K-means clustering은 데이터를 입력받아 이를 소수의 그룹으로 묶는 알고리즘이다. 이 알고리즘은 아래의 [그림 1]처럼 label이 없는 데이터를 입력받아 각 데이터에 label을 할당함으로써 군집화를 수행한다. K-means clustering은 개념과 구현이 매우 간단한 기본적인 clustering 알고리즘이면서도 실행 속도가 빠르고, 특정한 형태의 데이터에 대해서는 매우 좋은 성능을 보여주기 때문에 많이 이용되고 있다.
K-means clustering은 벡터의 형태로 표현된 $N$개의 데이터 $X = \{x_1, x_,2, ..., x_N\}$에 대하여 데이터가 속한 cluster의 중심과 데이터 간의 거리의 차이가 최소가 되도록 데이터들을 $K$개의 cluster $S = \{s_1, s_2, ..., s_K\}$에 할당한다. 많은 연구에서 $K$를 자동으로 설정하기 위한 시도가 이루어졌지만, 기본적으로 $K$는 데이터를 분석하고자 하는 사람이 직접 설정해주어야 한다. 어떠한 방법을 통해 $K$를 설정하였다고 가정할 때, k-means clustering의 동작은 아래의 최적화 문제로 표현될 수 있다.
$r_{nk}$는 $n$번째 데이터가 $k$번째 cluster에 속하면 1, 아니면 0인 값을 갖는 binary variable이며, $c_k$는 $k$번째 cluster의 중심을 뜻한다. k-means clustering을 실행한다는 것은 주어진 데이터 $X$에 대하여 $r_{nk}$와 $c_k$ 값을 설정하는 것과 같다.
위의 식 (1)의 형태로 표현된 k-means clustering 문제를 풀기 위한 방법으로는 1957년에 Stuart Lloyd가 제안한 Lloyd 알고리즘이 가장 많이 이용되고 있다. 주어진 데이터 $X$와 $k$에 대하여 k-means clustering 문제를 풀기 위한 Lloyd 알고리즘은 아래의 [알고리즘 1]과 같다.
Lloyd 알고리즘을 이용한 k-means clustering은 크게 initialization, assignment, update 부분으로 구성된다.
Initialization: 초기 $c_k$을 설정한다. 랜덤 초기화, Forgy 알고리즘, MacQueen 알고리즘 등 $c_k$를 초기화하기 위한 다양한 알고리즘들이 제안되었으며, 가장 기본적인 알고리즘은 랜덤 초기화이다. [알고리즘 1]에서는 1번째 줄에서는 랜덤 초기화를 이용하여 $c_k$의 초기값을 설정하고 있다.
Assignment: [알고리즘 1]의 4~6번째 줄과 같이 모든 데이터에 대하여 가장 가까운 cluster를 선택한다. 데이터와 cluster간의 거리는 데이터 벡터 $x_n$과 cluster의 중심 $c_k$간의 거리로 계산된다.
Update: 모든 데이터에 대하여 가장 가까운 cluster가 선택되면, 이를 바탕으로 $c_k$를 수정한다. 이 단계에서 $c_k$는 [알고리즘 1]의 8~10번째 줄과 같이 $k$번째 cluster $s_k$에 할당된 모든 데이터 벡터의 평균으로 갱신된다.
K-means clustering의 최적 해를 찾는 것은 NP-hard 문제에 속한다. 따라서, k-means clustering에서는 Lloyd 알고리즘과 같은 휴리스틱 (heuristic) 기법을 주로 이용한다. 데이터 벡터의 수가 $N$, 차원이 $D$인 데이터에 대하여 Lloyd 알고리즘을 이용하는 k-means clustering의 시간 복잡도는 $O(NKDI)$가 된다. 그러나 보통 $K$는 $N$보다 매우 작은 값으로 설정되고, assignment step과 update step의 반복 횟수인 $I$ 또한 $N$보다 매우 작은 값으로 설정되기 때문에 k-means clustering은 데이터의 수에 대하여 선형 시간복잡도를 갖는다. 이러한 특성 때문에 k-means clustering은 대규모 데이터를 처리하는 데 많이 이용되고 있다.
이 항목에서는 아래의 [그림 2]와 같은 2차원 데이터에 대해 k-means clustering의 동작을 단계별로 설명한다. Cluster의 수인 $K$는 2로 설정되었다고 가정한다.
1) [Initialization]: 초기 cluster의 중심을 랜덤하게 초기화한다. $c_1 = (4,3)$, $c_2 = (7,9)$로 초기화 되었다고 가정한다.
2) [Assignment]: 각 데이터 벡터 $x_n$과 cluster의 중심 $c_k$간의 거리를 계산한다. 그다음, 데이터를 가장 가까운 cluster에 할당한다. 각 데이터와 초기 cluster에 대한 거리를 계산하면 아래의 [표 2]와 같다.
이 과정에서 $x_1, x_4, x_6, x_7$은 $s_1$에 군집되고, $x_2, x_3, x_5$는 $s_2$에 군집된다.
3) [Update]: $c_1$과 $c_2$를 [알고리즘 1]의 9번째 줄과 같이 갱신한다. 이 과정에서 $c_1 = (2,1.75)$, $c_2 = (6.3333,7)$로 변경된다.
4) [Assignment]: cluster에 변화가 있었으므로, assignment와 update를 반복한다. 각 데이터와 갱신된 $c_1$, $c_2$에 대해 거리를 계산하면, [표 3]과 같이 거리가 계산된다. 이 과정에서 $x_1, x_4, x_6, x_7$은 $s_1$에 군집되고, $x_2, x_3, x_5$는 $s_2$에 군집된다.
5) [Update]: $c_1$과 $c_2$는 각각 (2, 1.75)과 (6.33,7)으로 계산된다. 그러나 $c_1$과 $c_2$의 변화가 없기 때문에 알고리즘을 종료한다.
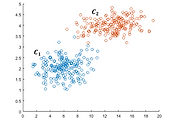
최종적으로 [그림 2]의 데이터에 대한 군집화 결과는 [그림 3]과 같으며, 주황색과 파란색은 군집의 종류, X 표시는 cluster의 중심을 의미한다.
'지능형시스템 > 데이터 마이닝' 카테고리의 다른 글
| [데이터 마이닝] DBSCAN과 밀도 기반 클러스터링 (1) | 2018.09.10 |
|---|---|
| [데이터 마이닝] 주성분 분석 (Principal Component Analysis, PCA)과 차원 축소 (2) | 2018.08.27 |