[머신 러닝] 앙상블 (Ensemble) 방법의 이해

1. 앙상블 (Ensemble) 방법

다양한 분야의 머신 러닝 문제를 챌린지의 형태로 해결하는 플랫폼인 Kaggle에서는 복잡한 딥 러닝 알고리즘보다 간단한 머신 러닝 모델을 앙상블 방법을 기반으로 결합한 알고리즘이 우승하는 것을 많이 볼 수 있다. 머신 러닝에서 앙상블은 단어 그대로 여러 단순한 모델을 결합하여 정확한 모델을 만드는 방법이다. 만약 머신 러닝 기술을 이용하여 실세계의 문제를 해결하고자 한다면 앙상블 방법을 반드시 이용할 수 있어야하며, 이는 앞서 설명한 바와 같이 Kaggle 챌린지에서 수 없이 증명되었다.

 

2. 가장 기본적인 앙상블 방법: 투표 기반 앙상블

강력한 성능에 비해 의외로 앙상블 방법의 개념은 매우 단순하다. 앙상블 개념의 핵심 개념은 다양한 종류의 여러 estimator를 결합하여 더 좋은 estimator를 만드는 것이다. 앙상블 방법의 종류는 estimator들을 어떻게 결합할 것인지에 의해 결정된다. 가장 단순한 앙상블 방법으로는 그림 2와 같이 투표를 기반으로 base estimator들을 결합하여 최종 estimator를 만드는 것이 있다.

 

그림 2. 투표 기반 앙상블 방법.

투표 기반 앙상블 방법에서는 다수의 예측이 곧 최종 예측이 되기 때문에 그림 2의 예시에서는 2가 아니라 1이라는 값이 최종 예측으로 선택되었다.

 

3. 투표 기반 앙상블 방법에 대한 이론적인 이해

이산확률분포를 이용하면 투표 기반 앙상블로 만들어진 최종 estimator의 오답률을 쉽게 계산해볼 수 있다. 만약 $N$개의 estimator들이 갖는 평균 정확도가 $p$이고 estimator들이 서로 독립적이라면, 투표를 기반으로 이러한 estimator들을 결합한 최종 estimator의 오답률 $P_e$는 다음과 같이 계산된다.

$$P_e = \sum_{k=\text{ceil}(N/2)}^{N}\binom{N}{k}(1-p)^k p^{(N-k)} \tag{1}$$

식 (1)에서 $k$를 $\text{ceil}(N/2)$부터 시작하는 이유는 과반수 이상의 estimator들이 오답을 내놓았을 때만 최종 estimator가 오답을 발생시키기 때문이다. 식 (1)이 의미하는 중요한 사실은 $p > 0.5$일 때 $N$이 증가할수록 $P_e$는 점점 감소한다는 것이다. 예를 들어, 그림 3은 정확도 $p$가 0.65일 때 $N$의 증가에 따른 $P_e$를 보여준다.

 

그림 3. 결합된 base estimator의 수에 따른 최종 estimator의 오답률

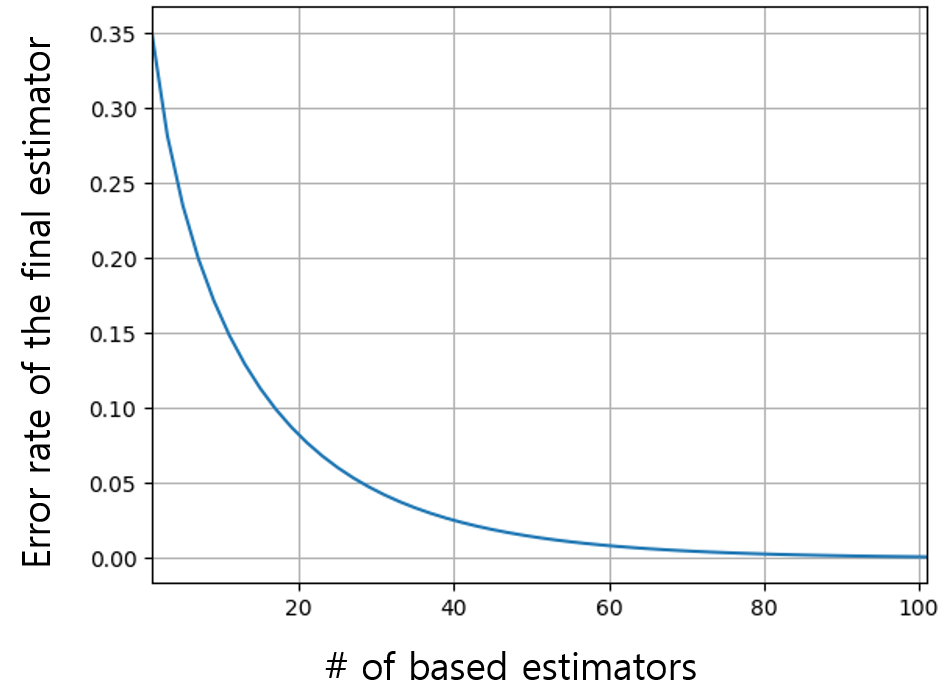
그림 3에서 볼 수 있듯이 평균 0.65의 정확도를 갖는 estimator를 11개 결합할 경우, 이론적으로 기존 오답률의 절반 수준에 해당하는 오답률 0.15를 얻을 수 있다. 주의할 점은 만약 정확도가 0.4밖에 되지 않는 estimator를 11개 결합한 경우에는 최종 estimator의 오답률이 0.75로 증가하기 때문에 반드시 어느 정도 정확한 estimator들을 결합해야 한다. 투표 이외에도 최대/최소를 이용한 결합이나 평균값을 이용한 방법 등 다양한 앙상블 방법이 존재한다. 이러한 방법에 대해 최종 estimator의 오답률에 대한 유도는 Combining Pattern Classifiers: Methods and Algorithms에 자세히 설명되어 있다.