[최적화] 입자 군집 최적화 (Particle Swarm Optimization, PSO)의 개념과 구현

1. 군집 기반 최적화 (Swarm-Based Optimization)

군집 기반 최적화는 수리적 최적화의 한 방법론으로써, 군집 기반 최적화에서는 여러 개의 optimizer가 서로 정보를 교환하며 동시에 최적화를 수행한다. 그림 1은 경사하강법 (gradient descent method)와 같은 single agent optimization과 PSO와 같은 swarm-based optimization의 차이를 개념적으로 보여준다.

그림 1. Single agent optimization (a)과 swarm-based optimization (b)의 차이. 그림에서 각 주황색 점은 주어진 법칙에 따라 함수의 최적해를 찾아가는 agent를 의미한다.

Single agent optimization에서는 주어진 법칙에 따라 최적해를 찾아간다. 대표적으로 경사하강법에서는 함수의 gradient를 따라 최적해를 찾아간다. 반면에 PSO와 같은 swarm-based optimization에서는 주어진 법칙에 더하여 agent 들이 저장하고 있는 정보를 조합하여 최적해를 찾아간다. 이러한 swarm-based optimization은 계산량이 많다는 단점이 존재하지만, 각 agent가 서로 정보를 교환하면서 최적화를 수행하기 때문에 하나의 agent가 local optimum에 빠지더라도 전체적으로는 global optimum에 수렴할 수도 있다는 장점이 있다. 아래의 그림 2는 군집 기반 최적화를 통해 2차원 함수의 최적점을 찾아가는 과정을 보여준다.

그림 2. 군집 기반 최적화를 이용한 최적점 탐색 (출처: https://commons.wikimedia.org/wiki/File:ParticleSwarmArrowsAnimation.gif).

 

2. 입자 군집 최적화 (Particle Swarm Optimization, PSO)

PSO에서는 $\mathcal{P}=\{\textbf{x}_1, \textbf{x}_2, ..., \textbf{x}_N\}$로 표현되는 $N$개의 입자 (particle)가 점진적으로 최적해를 찾아간다 [1]. 최종적으로는 $\mathcal{P}$ 중에서 가장 좋은 점수를 보여주는 solution이 PSO의 출력이 된다. PSO에서 $i$번째 입자의 위치 $\textbf{x}_i$는 식 (1)과 같이 입자의 속도 $\textbf{v}_i$를 더함으로써 업데이트된다.

$$\textbf{x}_i^{(k+1)} \leftarrow \textbf{x}_i^{(k)} + \textbf{v}_i^{(k+1)}. \tag{1}$$

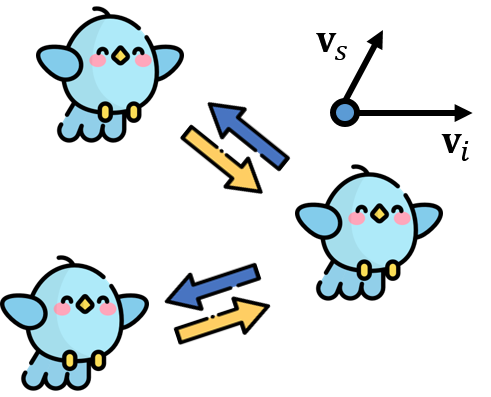
이때 속도는 그림 3과 같이 해당 입자의 현재 속도 $\textbf{v}_i$뿐만 아니라, 다른 입자들의 상태가 고려된 속도 $\textbf{v}_s$를 종합적으로 고려하여 결정된다 [2].

그림 3. 입자의 속도를 결정하기 위한 정보 교환.

PSO는 크게 알고리즘 초기화, 속도 계산, 위치 업데이트, 점수 평가라는 4가지 과정으로 구성된다. 알고리즘 초기화 이후에는 속도 계산, 위치 업데이트, 점수 평가라는 3가지 과정을 반복하여 최적해를 찾는다. 각 과정에 대한 자세한 설명은 아래에 있다.

 

2.1. 알고리즘 초기화 (Initialization)

랜덤 함수를 이용하여 입자의 초기 위치 $\textbf{x}_i^{(0)}$와 초기 속도 $\textbf{v}_i^{(0)}$를 초기화한다. 이 과정에서 $\textbf{v}_i^{(0)}$는 [$\textbf{b}_{lb}$, $\textbf{b}_{ub}$] 범위에 존재하는 임의의 값으로 설정한다. 이때 $\textbf{b}_{lb}$와 $\textbf{b}_{ub}$는 사용자가 PSO에 입력해주어야 하는 값으로써, 각각 solution이 존재할 수 있는 공간의 하한 (lower bound)과 상한 (upper bound)를 의미한다.

 

2.2. 속도 계산 (Velocity Calculation)

입자들의 현재 위치와 속도에 대해 다음 시간에서의 속도를 계산한다. 속도를 계산한다는 것은 현재 solution이 업데이트될 방향을 결정하는 것이기 때문에 경사하강법에서 목적 함수의 gradient를 구하는 것과 동일한 작업이다. 그러나 PSO에서는 그림 3과 같이 해당 입자의 상태만을 이용하는 것이 아니라, 군집에 속하는 모든 입자들로부터 만들어지는 정보를 같이 활용한다. PSO에서는 $i$번째 입자의 속도를 계산할 때마다 아래와 같이 입자 개인의 정보가 갖는 중요도 $\textbf{r}_1$와 군집 전체가 공유하는 정보의 중요도 $\textbf{r}_2$를 랜덤하게 설정한다.

$$\textbf{r}_1 \sim U(0, \phi_1) \tag{2},$$

$$\textbf{r}_2 \sim U(0, \phi_2) \tag{3}.$$

이때 $\phi_1$과 $\phi_2$는 사용자가 설정해주어야 하는 값으로써, 입자 개인의 정보와 군집 전체의 정보에 대한 중요도를 결정하는 역할을 한다.

계산된 $\textbf{r}_1$과 $\textbf{r}_2$에 대해 $i$번째 입자의 속도는 아래의 식 (4)와 같이 업데이트된다.

$$\textbf{v}_i^{(k+1)} \leftarrow \textbf{v}_i^{(k)} + \textbf{r}_1(\textbf{p}_i - \textbf{x}_i^{(k)}) + \textbf{r}_2(\textbf{g} - \textbf{x}_i^{(k)}). \tag{4}$$

위의 식에서 $\textbf{p}_i$는 $i$번째 입자가 현재의 시간 $k$까지 solution space를 탐색하면서 찾았던 최고의 위치 (solution)이며, $\textbf{g}$는 군집 전체에서 현재까지 찾았던 최고의 위치이다. 이러한 $\textbf{p}_i$와 $\textbf{g}$는 다음의 점수 평가 과정에서 설정된다.

그림 4. PSO의 속도 업데이트에 대한 기하학적 해석. a: 각 변수에 대한 업데이트 요소들. b: 입자 개인의 정보를 적용한 속도 업데이트. c: 입자 개인과 군집 전체의 정보를 모두 적용한 속도 업데이트.

그림 4는 식 (4)의 속도 업데이트 방식에 대한 기하학적 의미를 보여준다. 그림 4-a는 하나의 예시로써 속도 업데이트에서 고려되는 변수들의 위치 및 크기 등을 나타낸다. 그림 4-b에서는 입자 개인이 그동안 관측했던 최적 위치인 $\textbf{p}_i$를 고려하여 현재의 속도를 업데이트 한 것이다. 그림 4-c는 입자 개인과 군집 전체가 관측했던 최적 위치를 모두 고려하여 입자의 다음 속도인 $\textbf{v}_i^{(k+1)}$을 결정한 것이다. 그림 4에서 알 수 있듯이 PSO에서는 입자의 현재 정보 $\textbf{v}_i^{(k)}$, 입자 개인의 기록 $\textbf{p}_i$, 그리고 군집 전체의 기록 $\textbf{g}$를 모두 고려하여 속도를 업데이트한다. 이러한 업데이트 방식을 통해 PSO에서는 하나의 입자가 local optimum에 빠지더라도 군집 전체의 정보인 $\textbf{g}$를 활용하여 local optimum에서 빠져나올 수 있는 것이다. 이러한 업데이트 방식때문에 PSO를 global optimization algorithm으로 분류하기도 한다.

 

2.3. 위치 업데이트 (Position Update)

이전 단계에서 계산한 속도 $\textbf{v}_i^{(k+1)}$을 이용하여 입자의 위치 $\textbf{x}_i$를 업데이트 한다. 이 과정은 경사하강법에서 gradient를 따라 현재의 solution을 업데이트 하는 것과 같다. 그러나 PSO에서는 식 (5)와 같이 새롭게 계산된 속도를 현재 위치에 더함으로써 solution을 업데이트한다.

$$\textbf{x}_i^{(k+1)} = \textbf{x}_i^{(k)} + \textbf{v}_i^{(k+1)}. \tag{5}$$

 

2.4. 평가 (Evaluation)

업데이트된 위치 $\textbf{x}_i^{(k+1)}$에 대해 점수를 계산한다. 점수는 목적 함수 $f:\mathcal{X}\rightarrow\mathbb{R}$에 $\textbf{x}_i^{(k+1)}$을 입력함으로써 계산한다. 만약 목적 함수를 최소화하는 것이 목표라면 아래의 식 (6)을 만족하는 경우 $\textbf{p}_i$를 $\textbf{x}_i^{(k+1)}$로 업데이트한다.

$$f(\textbf{x}_i^{(k+1)}) < f(\textbf{p}_i). \tag{6}$$

만약 식 (6)을 만족하는 경우에는 업데이트된 $\textbf{p}_i$에 대해 식 (7)을 검사한다. 식 (7)을 만족하는 경우에는 $\textbf{g}$를 $\textbf{p}_i$로 업데이트한다.

$$f(\textbf{p}_i) < f(\textbf{g}). \tag{7}$$

평가 단계가 끝나면 사용자가 설정한 종료 조건을 확인한다. 종료 조건이 만족되는 경우에는 PSO를 종료하고, 아닌 경우에는 2.2의 속도 계산으로 돌아가 속도 계산, 위치 업데이트, 평가의 단계를 반복한다.

 

3. 정리

아래의 알고리즘 1은 앞에서 설명한 PSO의 각 과정을 코드 형식으로 정리한 것이다. PSO를 정리하자면 PSO는 목적 함수 $f$를 종료 조건 $\psi$를 만족할 때까지 최적화하면서 최종적으로 최적의 solution $\textbf{g}$를 얻기 위한 알고리즘이다.

알고리즘 1. PSO의 전체적인 동작에 대한 코드.

이 글에서 설명한 기본적인 PSO 이외에도 식 (4)의 $v_i^{(k)}$ 업데이트 식을 변형하거나 식 (5)에 학습률 (learning rate)를 추가한 형태의 다양한 PSO가 제안되었다. Python으로 PSO를 이용하고자 한다면 MEALPY라는 라이브러리를 추천한다.

 

 

참고문헌

[1] Bonyadi, M. R. and Michalewicz, Z. (2017). Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evolutionary Computation. 25 (1): 1-54.

[2] Dan Simon (2013). Evolutionary Optimization Algorithms. Wiley.