Graph attention network (GAT) [1]를 이해하기 위해서는 먼저 self-attention mechanism에 대한 이해가 필요하다. 아래의 그림 1은 구글 AI 블로그의 예제를 이용하여 자연어 처리에서 self-attention이 어떻게 정의되고 이용되는지를 보여준다.

자연어 처리에서는 'it', 'them', '그것'과 같이 문맥을 고려해야 단어가 무엇을 의미하는지 알 수 있는 경우가 많다. 그림 1의 예제에서도 'it'이라는 단어가 'animal'을 의미하는지 'street'을 의미하는지 알기 위해서는 같이 입력된 문장 전체를 고려해야 한다. Self-attention은 어떠한 입력을 이해하기 위해 같이 입력된 요소들 중에서 무엇을 중요하게 고려해야 하는지를 수치적으로 나타내는 기법이다. GAT은 이러한 self-attention mechanism을 노드 embedding 과정에 적용한 인공신경망이다.
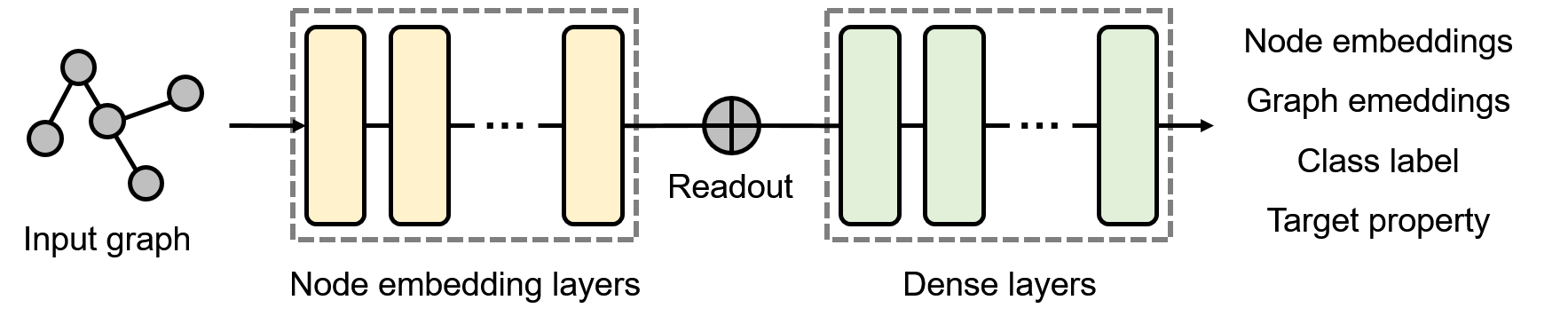
GAT은 기존의 graph neural network (GNN)과 유사하게 그림 2처럼 노드 embedding layer와 dense layer로 구성된다. 입력 그래프에 대해 노드 embedding layer에서는 각 노드에 대한 embedding을 생성한다. Readout은 그래프 단위의 출력을 만드는 경우에만 존재하는 계층으로써 전체 노드에 대한 노드 embedding을 모두 더하거나 평균을 내는 방식으로 그래프 전체의 embedding을 생성한다. 마지막으로, dense layer에서는 주어진 노드 또는 그래프 embedding에 대해 출력이 계산된다. Dense layer의 출력으로는 노드 또는 그래프의 embedding뿐만 아니라, 노드 또는 그래프에 대한 class label 및 target property 등이 될 수도 있다.
가장 대표적인 GNN인 graph convolutional network (GCN)에서는 노드 embedding layer가 graph convolution이라는 연산으로 정의되었지만, GAT에서는 self-attention으로 노드 embedding layer가 정의된다. 즉 GAT은 어떠한 노드의 embedding을 생성할 때 인접한 노드들에 대한 중요도를 계산하여 이를 기반으로 새로운 embedding 만든다. 이는 그림 1에서 'it'이라는 단어의 의미를 파악할 때 같이 입력된 단어들의 중요도를 보는 것과 비슷한 개념이다.
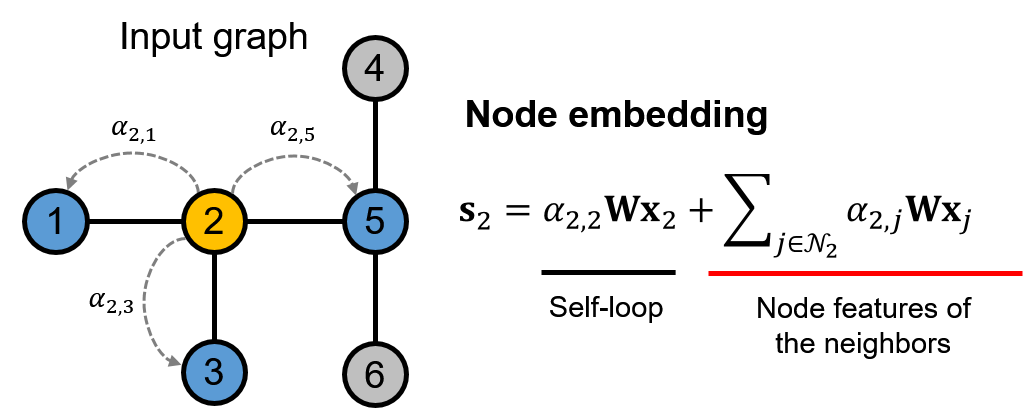
그림 3은 self-attention 기반의 노드 embedding $\textbf{s}_i$를 생성하기 위한 과정을 보여준다. 그림에서 $W$는 학습 가능한 가중치 행렬, $\textbf{x}_i$는 $i$번 노드의 feature, $\alpha_{i,j}$는 $i$번 노드에서 $j$번째 노드로의 attention 값을 의미한다. 마지막으로, $\mathcal{N}_i$는 $i$번 노드와 edge로 연결된 인접 노드들의 index set이다. 그림 3의 예시에서는 2번 노드에 대해 attention 기반의 node embedding $\textbf{s}_2$를 생성한다. 이 과정에서 인접한 1, 3, 5번 노드에 대해 attention score를 계산하여 이를 기반으로 $\textbf{s}_2$를 생성하기 위한 weighted sum을 수행한다. 생성된 node embedding $\textbf{s}_2$에 대해 활성 함수 $f$를 적용함으로써 최종 node embedding인 $\textbf{h}_2 = f(\textbf{s}_2)$를 계산한다. 이러한 self-attention 기반의 노드 embedding을 수행하는 계층을 GAT에서는 graph attention layer라고 하며, 다음 항목에서는 GAT의 각 계층을 수식적으로 서술한다.
Graph attention layer는 그림 3과 같이 self-attention을 기반으로 노드 embedding을 생성하는 계층이다. GAT에서 $k$번째 graph attention layer의 출력 $\textbf{h}_i^{(k)}$은 다음과 같이 정의된다.
$$\textbf{s}_i^{(k)} = \alpha_{i,i}^{(k)}\textbf{W}^{(k)}\textbf{h}_i^{(k-1)} + \sum_{j\in\mathcal{N}_i} \alpha_{i,j}^{(k)}\textbf{W}^{(k)}\textbf{h}_j^{(k-1)}, \tag{1}$$
$$\textbf{h}_i^{(k)} = f_k(\textbf{s}_i^{(k)}). \tag{2}$$
위의 식에서 $\mathcal{N}_i$는 $i$번째 노드에 대한 인접 노드들의 index이며, $\textbf{W}^{(k)}$와 $f_k$는 각각 $k$번째 graph attention layer의 가중치 행렬과 활성 함수이다. $\textbf{h}_i^{(k-1)}$은 이전 graph attention layer의 출력으로써 $\textbf{h}_i^{(0)}$은 $\textbf{x}_i$로 표현되는 입력 node-feature이다. 마지막으로, 식 (1)의 attention score $\alpha_{i,j}^{(k)}$는 다음의 식 (3)과 같이 정의된다.
$$\alpha_{i,j}^{(k)} = \frac{\exp\left(\phi^{(k)}(\textbf{W}^{(k)}\textbf{h}_i^{(k)},\textbf{W}^{(k)}\textbf{h}_j^{(k)}) \right)}{\sum_{r\in\mathcal{N}_i} \exp\left(\phi^{(k)}(\textbf{W}^{(k)}\textbf{h}_i^{(k)},\textbf{W}^{(k)}\textbf{h}_r^{(k)}) \right)}. \tag{3}$$
식 (3)에서 $\phi^{(k)}: \mathcal{Z}\times\mathcal{Z} \rightarrow \mathbb{R}$는 $k$번째 graph attention layer의 attention 함수로써, 논문에서는 Leaky ReLU를 기반으로 식 (4)와 같이 정의되었다.
$$\phi^{(k)}(\textbf{W}^{(k)}\textbf{h}_i^{(k)},\textbf{W}^{(k)}\textbf{h}_j^{(k)}) = \text{LeakyReLU}\left(\textbf{a}_k^T [\textbf{W}^{(k)}\textbf{h}_i^{(k)}\oplus\textbf{W}^{(k)}\textbf{h}_j^{(k)}]\right). \tag{4}$$
위의 식에서 $\textbf{a}_k$는 학습 가능한 가중치 벡터이고, $\oplus$는 벡터 접합 (vector concatenation) 연산을 의미한다. 요약하자면, graph attention layer는 학습 가능한 가중치 행렬 $\textbf{W}^{(k)}$와 attention 함수의 가중치 벡터 $\textbf{a}_k$를 기반으로 식 (1)-(4)의 과정을 통해 새로운 노드 embedding $\textbf{h}_i^{(k)}$를 생성한다.
GNN에서 readout은 생성된 노드 embedding을 하나의 벡터로 변환하여 그래프 전체의 embedding을 생성하는 기능을 수행한다. 따라서, GAT을 비롯한 GNN을 이용하여 노드에 대한 embedding, classification, regression을 수행하고자 하는 경우에는 GNN 구조에 readout이 포함되지 않는다. 그러나 그래프 embedding이나 분자 속성 예측과 같이 그래프 단위의 작업을 수행할 때는 readout이 GNN 구조에 포함되어야 한다.
일반적으로 readout은 모든 노드들의 embedding을 평균내거나 더함으로써 그래프 embedding을 생성한다. 예를 들어, 가장 많이 이용되고 있는 평균값 기반의 readout 함수 $\phi:\mathbb{R}^{N\times m} \rightarrow \mathbb{R}^m$은 다음의 식 (5)와 같이 정의된다.
$$\phi(\textbf{H}^{(K)}) = \left[\frac{1}{N}\sum_{i=1}^{N}\textbf{h}_{i,1}^{(K)}, \frac{1}{N}\sum_{i=1}^{N}\textbf{h}_{i,2}^{(K)} ..., \frac{1}{N}\sum_{i=1}^{N}\textbf{h}_{i,m}^{(K)}\right]. \tag{5}$$
식 (5)에서 $N$은 그래프에 포함된 노드의 수, $m$은 마지막 $K$번째 node embedding layer의 출력 차원이다. 기존 GNN과 GAT의 차이점은 node embedding layer에 있기 때문에 GAT의 readout은 기존의 GNN과 동일한 함수들을 이용한다.
기존 GNN과 동일하게 GAT에서도 그림 2와 같이 node embedding 다음에 dense layer가 순차적으로 구현된다. Dense layer는 fully-connected layer로 구현되며, 입력된 노드 embedding 행렬 또는 그래프 embedding 벡터에 대한 출력을 계산한다. 따라서, 첫 번째 dense layer의 입력 차원은 마지막 node embedding layer의 출력 차원과 같은 $m$이어야 한다.
[1] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. (2018). Graph Attention Networks. International Conference on Learning Representation.
'지능형시스템 > 머신러닝' 카테고리의 다른 글
| [머신 러닝/딥 러닝] Metric Learning의 개념과 Deep Metric Learning (1) | 2020.09.06 |
|---|---|
| [머신 러닝/딥 러닝] CGCNN: 인공지능과 소재 개발 (Artificial Intelligence and Material Discovery) (4) | 2020.03.20 |
| [머신 러닝] 과적합 (Overfitting)과 Validation Dataset의 개념 (12) | 2019.12.25 |
| [머신 러닝] 앙상블 (Ensemble) 방법의 이해 (0) | 2019.12.24 |
| [머신 러닝/딥 러닝] 인공신경망 (Artificial Neural Network, ANN)의 종류와 구조 및 개념 (3) | 2019.12.23 |




