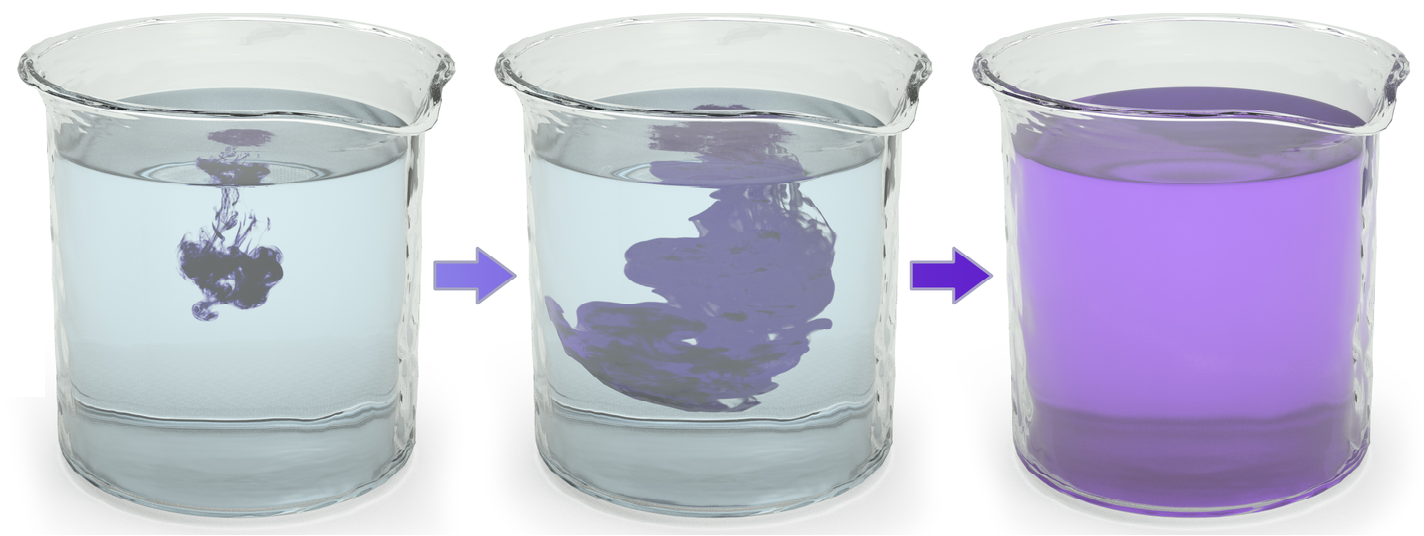
자연계에서는 그림 1과 같이 초기에는 특정 분포에 따라 존재하던 입자가 최종적으로 균일하게 분포하는 확산 (diffusion) 현상이 발생한다. Diffusion model은 이러한 자연계의 확산 과정을 기반으로 고안된 생성형 머신러닝 방법론이다 [1].
Diffusion model은 기본적으로 그림 2와 같이 forward process와 reverse process로 구성된다. Forward process는 원본 데이터 $x_0$를 최종 노이즈 $x_T$로 변환하는 과정이고, reverse process는 최종 노이즈 를 원본 데이터 $x_0$로 변환하는 과정이다. Diffusion model은 reverse process를 학습함으로써 임의의 노이즈 $x_T$로부터 데이터 $x_0$를 만들어내는 생성형 모델로 사용될 수 있다.

Denoising diffusion probabilistic model (DDPM) [2]은 forward process와 reverse process를 확률 과정으로 정의하였으며, diffusion model의 동작을 이해하는데 기초가 되는 방법론이다. 이 글에서는 DDPM의 구조와 DDPM을 유도하기 위한 수학적 과정에 대해 소개한다.
Forward process의 목적은 원본 데이터 $x_0$를 최종 noise $x_T$로 변환하는 것이다. Forward process는 새로운 데이터를 생성하는 reverse process를 학습할 때 이용된다. Forward process는 Markov chain을 기반으로 아래의 식 $\eqref{eq:forward_proc}$과 같이 정의된다.
$$\begin{equation} q(x_T, x_{T-1}, ..., x_1|x_0) = \prod_{t=1}^T q(x_t|x_{t-1}). \label{eq:forward_proc} \end{equation}$$
일반적으로 foward process를 구성하는 각 확률분포 $q(x_t|x_{t-1})$는 식 $\eqref{eq:forward_proc_norm}$와 같이 정규 분포 (normal distribution)를 기반으로 정의된다.
$$\begin{equation} q(x_t|x_{t-1}) = \mathcal{N}(x_t ; \sqrt{1-\beta_t}x_{t-1}, \beta_t\textbf{I}) \label{eq:forward_proc_norm}. \end{equation}$$
$\beta_1, ..., \beta_T \in (0, 1)$는 원본 데이터 $x_0$에 Gaussian noise를 더해가는 속도를 조절하는 hyperparameter이다. 식 $\eqref{eq:forward_proc_norm}$과 같이 forward process를 정의하면, 원본 데이터 $x_0$가 주어졌을 때 $q(x_t|x_0)$에서 $x_t$를 바로 샘플링할 수 있다는 장점이 있는데, 자세한 내용은 아래에서 설명한다.
Reverse process의 목적은 최종 noise $x_T$에서 원본 데이터 $x_0$를 복원하는 것이다. Diffusion model의 핵심은 주어진 데이터셋으로부터 reverse process를 학습하고, 이를 바탕으로 noise로부터 새로운 데이터를 생성하는 것이다. Reverse process도 Markov chain을 기반으로 식 $\eqref{eq:reverse_proc}$와 같이 정의된다.
$$\begin{equation} p(x_0, x_1, ..., x_T) = p(x_T)\prod_{t=1}^T p(x_{t-1}|x_t). \label{eq:reverse_proc} \end{equation}$$
위의 Reverse process에 대해 process의 시작점인 noise $x_T$의 확률분포 $p(x_T)$는 식 $\eqref{eq:noise_dist}$와 같이 가정한다.
$$\begin{equation} p(x_T) = \mathcal{N}(x_T; \textbf{0}, \textbf{I}). \label{eq:noise_dist} \end{equation}$$
그 다음, 각 확률분포를 식 $\eqref{eq:prob_rev_proc}$과 같이 매개변수화된 정규분포로 정의한다.
$$\begin{equation} p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \boldsymbol{\mu}_\theta(x_t, t), \boldsymbol{\Sigma}_\theta(x_t, t)). \label{eq:prob_rev_proc} \end{equation}$$
위의 식에서 $\boldsymbol{\mu}_\theta(x_t, t)$와 $\boldsymbol{\Sigma}_\theta(x_t, t)$는 일반적으로 $x_t$와 $t$를 입력으로 출력을 생성하는 인공신경망으로 정의된다.
DDPM의 목적은 reverse process를 통해 새로운 데이터를 생성하는 것이기 때문에 DDPM은 아래와 같이 확률분포 $p_\theta(x)$의 log-lilkelihood를 최대화하도록 학습이 이루어진다.
$$\begin{equation} \theta^* = \underset{\theta}{\text{argmax}} \; \mathbb{E}[\log p_\theta(x)]. \label{eq:obj_func} \end{equation}$$
대부분의 문제에서 DDPM의 목적 함수를 바로 계산하는 것은 불가능하기 때문에 아래의 과정을 통해 목적 함수의 하계 (lower bound)를 구하고, 하계를 최대화함으로써 DDPM의 학습을 진행한다.
$$\begin{align} \log p(x) &= \log \int p(x_{0:T})dx_{1:T}\nonumber\\ &= \log \int \frac{p(x_{0:T})q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)} dx_{1:T}\nonumber\\ &\geq \mathbb{E}_{q(x_{1:T}|x_0)} \left[\log \frac{p(x_{0:T})}{q(x_{1:T}|x_0)} \right] := J. \label{eq:obj_1} \end{align}$$
DDPM의 모델링에 해당하는 식 $\eqref{eq:forward_proc}$과 $\eqref{eq:reverse_proc}$에 의해 목적 함수의 하계 $J$는 아래와 같이 계산 가능한 형태로 변형된다.
$$\begin{align} J &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log \frac{p(x_T) \prod_{t=1}^T p_\theta(x_{t-1}|x_t)}{\prod_{t=1}^T q(x_t|x_{t-1})} \right]\nonumber\\ &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log \frac{p(x_T) p_\theta(x_0|x_1) \prod_{t=2}^T p_\theta(x_{t-1}|x_t)}{q(x_1|x_0) \prod_{t=2}^T q(x_t|x_{t-1})} \right]\nonumber\\ &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log \frac{p(x_T) p_\theta(x_0|x_1) \prod_{t=2}^T p_\theta(x_{t-1}|x_t)}{q(x_1|x_0) \prod_{t=2}^T q(x_t|x_{t-1}, x_0)} \right]\nonumber\\ &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[\log \frac{p(x_T)p_\theta(x_0|x_1)}{q(x_1|x_0)} + \log \prod_{t=2}^T \frac{p_\theta(x_{t-1}|x_t)}{\frac{q(x_t, x_{t-1}, x_0)q(x_t,x_0)q(x_0)}{q(x_{t-1},x_0)q(x_t,x_0)q(x_0)}} \right]\nonumber\\ &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log \frac{p(x_T)p_\theta(x_0|x_1)}{q(x_1|x_0)} + \log \prod_{t=2}^T \frac{p_\theta(x_{t-1}|x_t)q(x_{t-1}|x_0)}{q(x_{t-1}|x_t,x_0)q(x_t|x_0)} \right]. \label{eq:obj_2} \end{align}$$
식 $\eqref{eq:obj_2}$의 두 번째 항을 전개하면, $\eqref{eq:obj_2}$은 아래와 같이 정리된다.
$$\begin{align} J &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[\log \frac{p(x_T)p_\theta(x_0|x_1)}{q(x_T|x_0)} + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} \right]\nonumber\\ &= \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log p_\theta(x_0|x_1)\right] + \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log \frac{p(x_T)}{q(x_T|x_0)} \right] + \sum_{t=2}^T \mathbb{E}_{q(x_{1:T}|x_0)}\left[ \log \frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)} \right]. \end{align}$$
기댓값의 정의와 DDPM의 Markov 속성을 이용하면 $q(x_{1:T}|x_0)$에 대한 기댓값을 아래와 같이 정리할 수 있으며, 이를 통해 실제 목적 함수를 계산하기 위해 어떠한 샘플을 추출해야하는지를 명확히 할 수 있다.
$$\begin{equation}J = \mathbb{E}_{q(x_1|x_0)}\left[\log p_\theta(x_0|x_1)\right] + \mathbb{E}_{q(x_T|x_0)}\left[\log\frac{p(x_T)}{q(x_T|x_0)} \right] + \sum_{t=2}^T\mathbb{E}_{q(x_t, x_{t-1}|x_0)}\left[ \log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)} \right]. \end{equation}$$
Kullback–Leibler divergence $D_{KL}$의 정의에 의해 최종 목적 함수는 아래와 같이 정의된다.
$$\begin{equation}J = \underbrace{\mathbb{E}_{q(x_1|x_0)}\left[\log p_\theta(x_0|x_1)\right]}_{\text{reconstruction term}} - \underbrace{D_{KL}(q(x_T|x_0)||p(x_T))}_{\text{prior matching term}} - \sum_{t=2}^T \underbrace{\mathbb{E}_{q(x_t|x_0)}\left[D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) \right]}_{\text{denoising matching term}}. \label{eq:obj_final} \end{equation}$$
따라서, DDPM의 매개변수 $\theta$는 식 $\eqref{eq:obj_final}$을 최대화함으로써 학습된다.
DDPM 학습의 목적 함수인 식 $\eqref{eq:obj_final}$의 각 항은 아래와 같이 해석될 수 있다.
- Reconstruction term: 주어진 데이터 $x_0$에 대해 $x_1$를 생성하고, 다시 $x_1$을 이용하여 $x_0$를 생성함으로써 계산할 수 있다. 이는 variational autoencoder (VAE)의 동작과 유사하며, 이러한 해석을 바탕으로 첫 번째 항을 reconstruction term으로 간주할 수 있다.
- Prior matching term: forward process의 최종 출력에 대한 분포 $x_T$와 식 $\eqref{eq:noise_dist}$에서 가정한 $x_T$의 사전 분포의 차이를 의미한다. 그러나 두 번째 항에는 학습 가능한 매개변수가 없기 때문에 DDPM의 학습 과정에서는 상수로 취급된다.
- Denoising matching term: 노이즈를 제거해나가는 과정 $p_\theta(x_{t-1}|x_t)$를 학습한다. $q(x_{t-1}|x_t,x_0)$는 최종적으로 노이즈가 제거된 데이터 $x_0$가 주어졌을 때의 노이즈 제거 과정을 의미하기 때문에 $q(x_{t-1}|x_t,x_0)$는 $p_\theta(x_{t-1}|x_t)$를 학습시키기 위한 ground truth 정보로 볼 수 있다.
복잡한 과정을 거쳐 DDPM의 목적 함수인 식 $\eqref{eq:obj_final}$을 유도했지만, 현재 상태로 목적 함수를 계산하는 것은 매우 어렵다. DDPM에서는 식 $\eqref{eq:forward_proc_norm}$과 $\eqref{eq:prob_rev_proc}$의 정규분포 가정을 바탕으로 식 $\eqref{eq:obj_final}$을 계산 가능한 형태로 변형한다.
먼저 Markov 가정에 의해 $q(x_t|x_{t-1},x_0) = q(x_t|x_{t-1})$로 생각할 수 있다. 그 다음 $\alpha_t = 1 - \beta_t$로 정의하면, 식 $\eqref{forward_proc_norm}$의 정규분포 가정과 reparameterization trick에 의해 $x_t$를 아래와 같이 계산할 수 있다.
$$\begin{equation} x_t = \sqrt(\alpha_t)x_{t-1} + \sqrt{(1 - \alpha_t)} \epsilon, \end{equation}$$
위의 식에서 $\epsilon \sim \mathcal{N}(\epsilon;\textbf{0}, \textbf{I})$인 랜덤값이다.
[1] Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. (2015, June). Deep unsupervised learning using nonequilibrium thermodynamics. In International conference on machine learning (pp. 2256-2265). pmlr.
'머신러닝 > 확률모델' 카테고리의 다른 글
| 편향-분산 트레이드오프 (Bias-Variance Tradeoff)와 L2 규제 (L2 Regularization) (5) | 2024.01.15 |
|---|---|
| Unbiased and Biased Estimators의 개념과 머신러닝 (1) | 2024.01.11 |
| 몬테카를로 방법 (Monte Carlo Method)과 베이지안 머신러닝 (3) | 2024.01.07 |
| [머신러닝] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)과 EM 알고리즘 (21) | 2023.12.29 |
| Reparameterization Trick에 대한 수학적 이해와 기댓값의 미분가능성 (2) | 2023.12.21 |