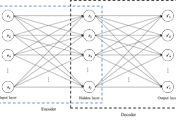
일반적인 neural network의 neuron은 가중치와 입력값, 출력값이 실수 도메인에 존재하며, 이러한 neural networks를 real-valued neural networks (RVNNs)라고 하고, RVNNs를 구성하는 각각의 neuron를 real-valued neuron (RVN)이라고 한다. 이 글에서 소개하는 complex-valued neuron (CVN)은 RVN과 같은 구조 및 데이터 처리 과정을 갖지만, 가중치와 입력값, 출력값이 복소 도메인에 존재한다.
CVN으로 이루어지는 complex-valued neural networks (CVNNs)는 현재까지도 많은 연구가 이루어지고 있는 분야이며, RVNNs에 비해 다소 복잡한 구조를 갖고 있다. 특히, 실수 도메인에 존재하는 입력값을 복소 도메인으로 변환하는 방법론과 뉴런의 출력값을 결정하는 활성함수 (activation function)를 정의하는 부분에 있어서 CVNNs는 RVNNs에 비해 더욱 복잡한 계산이나 더 많은 단계의 처리를 필요로 하는 것이 일반적이다.
비록 CVN 및 CVNNs는 RVN과 RVNNs 보다 다소 복잡한 구조를 갖고 있지만, CVN은 RVN이 해결할 수 없는 선형 분류가 불가능한 문제를 해결할 수 있는 등, CVN에는 복소체계를 이용함으로써 존재하는 여러 장점들이 있다. 이러한 장점들 때문에 CVN 및 CVNNs을 회로 분석과 신호 처리 등, 복소체계를 이용하는 다양한 분야에 적용하기 위한 연구가 진행되고 있으며, 최근에는 다양한 데이터 분류 및 인식 문제에도 적용되고 있다. CVNNs가 갖는 장점을 간략하게 요약하면 아래와 같다.
인간의 뇌에서는 다양한 위상의 신호가 감지되는데, 복소체계는 이러한 현상을 모델링하기에 적합하다.
RVN은 1차원 데이터만 처리할 수 있는 반면에 CVN은 기본적으로 2차원 데이터까지 처리할 수 있다.
CVNNs에서 이용되는 역전파 알고리즘은 일반적으로 RVNNs에서 이용되는 역전파 알고리즘보다 2~3배 학습 속도가 빠르다.
일반적으로, 같은 문제에 대해서 CVNNs은 RVNNs에 비해 가중치, 임계값 (threshold) 등과 같은 인자를 절반만 필요로 한다.
CVN은 실수 도메인에서 정의된 RVN과 흡사한 구조를 갖는다. [그림 1]의 (a)는 일반적인 neuron인 RVN의 구조를 나타낸 것이며, (b)는 이 글에서 소개하는 CVN의 구조를 나타낸 것이다.
[그림 1] RVN과 CVN의 구조
[그림 1]에 나타나듯이 RVN과 CVN의 구조는 거의 같다. 그러나 CVN은 $net$값을 계산하기 전에 실수 도메인의 입력 벡터를 복소화 (complexification)하는 추가적인 작업을 수행한다.
CVN에서는 $net$값을 계산하기 전에 입력 데이터를 복소화하는 작업을 수행한다. 입력 데이터를 복소화하는 방법은 다양한 방법이 존재할 수 있으며, 복소화하는 방법에 따라 성능상의 차이가 발생하기도 한다.
복소화의 방법으로는 다음의 [식 1] 같은 변환이 있을 수 있으며, 이러한 변환은 다양한 복소화 방법 중에서 하나의 예시일 뿐이다. [식 1]에서 $x$는 입력 데이터이고, $a$와 $b$는 실수 도메인에 존재하는 상수이다.
[식 1]과 같은 변환을 통해 실수 도메인에 존재하였던 입력 데이터 $x$는 복소 도메인의 데이터로 변환된다.
CVN의 활성함수는 복소수로 표현된 net값을 실수 도메인의 값으로 변환하는 역할을 한다. CVN에서는 활성함수 또한 복소화 방법과 마찬가지로 다양한 형태의 함수가 존재할 수 있으며, 활성함수의 형태에 따라 CVN의 정확도가 변동하기도 한다. 아래의 [식 2]는 CVN에서 이용되는 활성함수의 형태를 나타내고, [식 3]은 CVN에서 활성함수로 이용될 수 있는 함수의 예시이다.
[식 3]에서 $u$와 $v$는 각각 복소수 $z$의 실수부 (real part)와 허수부 (imaginary part)를 의미한다.
References
[1] Md. Faijul Amin, Kazuyuki Murase. 2009. Single-Layered Complex-Valued Neural Network for Real-Valued Classification Problems. Neurocomputing 72 (2009), pp. 945-955.
[2] Hans Georg Zimmermann, Alexey Minin, Victoria Kusherbaeva. 2011. Comparison of the Complex Valued and Real Valued Neural Networks Trained with Gradient Descent and Random Search Algorithms. ESANN 2011 proceedings, European Symposium on Artificial Neural Networks, April 2011, pp. 213-218.
'지능형시스템_' 카테고리의 다른 글
| [머신 러닝] - 은닉 마르코프 모델 (Hidden Markov Model, HMM) (11) | 2016.09.02 |
|---|---|
| [머신러닝] - Autoencoder (3) | 2016.07.30 |
| [머신러닝] - Overfitting (과적합) (0) | 2016.05.07 |
| [지능형시스템] - Artificial Bee Colony(ABC) Algorithm (0) | 2016.04.13 |
| [머신러닝] - LVQ(Learning Vector Quantization) (0) | 2016.04.08 |