[머신 러닝] - 은닉 마르코프 모델 (Hidden Markov Model, HMM)

Markov model은 어떠한 날씨, 주식가격 등과 같은 어떠한 현상의 변화를 확률 모델로 표현한 것이다. Hidden Markov model (HMM)은 이러한 Markov model에 은닉된 state와 직접적으로 확인 가능한 observation을 추가하여 확장한 것이다. HMM은 observation을 이용하여 간접적으로 은닉된 state를 추론하기 위한 문제를 풀기 위해 사용된다.
아래의 [그림 1]은 은닉된 state와 그에 따른 observation의 개념을 나타낸다. HMM을 이용해 우리가 풀고자 하는 문제는 관측 가능한 것은 오직 $y_t$뿐이며, $y_t$는 $q_t$에 종속적으로 발생한다고 할 때, $y_t$의 sequence를 통해 $q_t$의 sequence를 추론하는 것이다.

[그림 1] 은닉된 state와 직접적으로 확인 가능한 observation

1950년대 이후 forward-backward recursion, Baum-Welch algorithm, Viterbi algorithm이 소개되면서 HMM에 대한 많은 연구가 진행되었고, 1970년대에는 음성 인식 분야에서 HMM이 활발히 응용되기 시작하였다. 현재는 필기체 인식, 동작 인식, 품사 태깅 등과 같이 이전 시간의 데이터에 영향을 받는 순차 데이터에서 패턴을 인식하기 위해 이용되고 있다.

1. HMM의 구조

HMM은 <$Q, Y, \pi, T, E$>라는 tuple로 정의되며, 각각의 요소가 의미하는 내용은 아래와 같다.

• $Q = \{q_1, q_2, ..., q_N\}$ - 은닉된 state들의 집합이다.
• $Y = \{y_1, y_2, ..., y_M\}$ - 은닉된 state에서 발생할 수 있는 observation들의 집합이다.
• $\pi: \mathbb{R}^{N}$ - 초기 state가 $q_i$일 확률을 나타내는 initial probability $p(q_i)$의 집합이다.
• $\boldsymbol{A}: \mathbb{R}^{N \times N}$ - $q_i$에서 $q_j$로 이동할 확률을 나타내는 transition probability $p(q_j|q_i)$의 집합이다.
• $\boldsymbol{B}: \mathbb{R}^{N \times M}$ - $q_i$에서 $y_j$가 발생할 확률을 나타내는 emission probability $p(y_j|q_i)$의 집합이다.

일반적으로 HMM은 아래의 [그림 1]과 같은 그래프의 형태로 표현된다. 그래프에서 $s_i$는 은닉된 state를 나타내며, $Q$에 있는 원소 중 한 가지 값을 갖는다. $o_j$는 $s_i$에서 발생한 observation을 의미하며, $Y$의 원소 중 한 가지 값을 갖는다.

 

[그림 2] 2개의 state와 3개의 observation을 갖는 HMM의 구조

HMM의 동작을 설명하기 위한 한 가지 예시로써 지출내역을 통해 과거의 행동을 유추하는 문제를 [그림 3]과 같은 HMM으로 정의할 수 있다. 오늘 하려는 행동은 무엇을 했는지에 영향을 받으며, 과거에 했던 행동은 과거로 돌아가지 않는 한 다시는 관측할 수 없기 때문에 과거의 행동은 은닉된 state에 해당한다. 이 예제에서 $Q = \{study, friend, game \}$으로, 각각 공부, 친구 만나기, 게임을 의미한다. 지출내역은 카드명세서를 통해 과거의 내역이더라도 직접적으로 관측할 수 있기 때문에 observation에 해당한다. 이 예제에서 $Y = \{1, 2, 3, 4 \}$이며, 값이 클 수록 돈을 많이 사용했다는 것을 의미한다.

 

[그림 3] 지출내역을 통해 과거의 행동을 추론하기 위한 HMM

HMM을 구성하기 위해서는 위에서 정의한 $Q$와 $Y$ 이외에도 HMM의 parameter에 해당하는 initial probabilities $\pi$, transition probabilities $\boldsymbol{A}$, emission probabilities $\boldsymbol{B}$를 추정해야 한다. 일반적으로 HMM의 parameter를 추정하기 위해서는 Baum-Welch algorithm이 사용되며, 이 예제에서는 $\pi, \boldsymbol{A}, \boldsymbol{B}$가 각각 아래의 [표 1, 2]와 같이 추정되었다고 가정한다. [표 1]에서 Initial 행은 initial probabilties를 나타낸다.

[표 1] Initial probabilities와 transition probabilities

 

[표 2] Emission probabilities

 

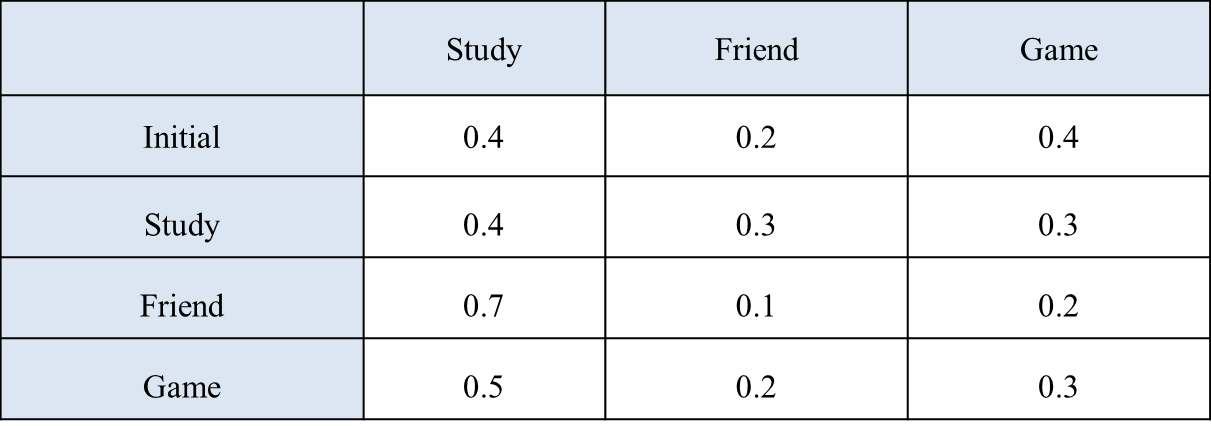
[표 1]을 통해서는 사람의 행동 양식을 알 수 있다. 예를 들어, 전날 친구를 만나고 오늘도 친구를 만날 확률은 0.1로 매우 작다는 것이나 전날 게임을 했다면 오늘은 0.5의 확률로 공부를 한다는 것이다. 또한, [표 2]를 통해서는 소비 습관을 알 수 있다. 예를 들어, 공부를 하는 날에는 돈을 거의 쓰지 않는다는 것이나 친구를 만나면 0.4의 확률로 많은 돈을 쓴다는 것이다. HMM은 이러한 확률적 사실들을 바탕으로 observation을 통해 은닉된 state를 추론하는 것이다.

2. HMM의 동작

[그림 3]과 [표 1, 2]로 정의된 HMM이 주어졌을 때, 우리는 HMM을 이용하여 아래의 두 가지 사항을 추론할 수 있다.

• 지출 내역이 1 1 4 2일 때, 이러한 지출 내역이 나타날 확률 계산
• 지출 내역이 1 1 4 2일 때, 이러한 지출 내역이 나타날 확률이 가장 큰 과거의 행동 추론

위와 같은 두 가지 동작은 결국 HMM을 이용하여 conditional probability를 계산하는 것과 같다. HMM을 구현할 때는 이러한 두 가지 추론 과정을 어떻게 구현할 것인지에 대해 고려해야 한다. 또한, [그림 3]의 예제에서는 HMM의 인자인 $\pi, \boldsymbol{A}, \boldsymbol{B}$가 주어졌다고 가정하였지만, 원래는 데이터로부터 HMM의 인자를 학습하는 과정을 거쳐야 하기 때문에 학습 연산 역시 HMM의 구현 시 고려되어야 하는 문제이다. 따라서, HMM을 구현할 때는 아래와 같은 3가지 문제를 풀기 위한 연산을 어떻게 구현할 것인지 생각해야 한다.

• HMM의 parameter가 주어졌을 때, 주어진 observation이 나타날 확률 계산
• HMM의 parameter가 주어졌을 때, 주어진 observation이 나타날 확률이 가장 높은 state의 나열을 계산
• 학습 데이터로부터 HMM의 parameter $\theta = \{ \pi, \boldsymbol{A}, \boldsymbol{B} \}$를 학습

첫 번째와 두 번째 문제는 각각 dynamic programming 기반의 forward algorithm과 Viterbi algorithm으로 해결할 수 있다. HMM의 parameter를 학습시키는 마지막 문제는 주로 expectation-maximization algorithm (EM algorithm)의 한 형태는 Baum-Welch algorithm으로 해결한다.

2.1. 주어진 observation이 나타날 확률 (likelihood) 계산: forward algorithm

첫 번째 문제는 HMM의 모든 parameter가 결정되었을 때, 주어진 observation $O = o_1, o_2, ..., o_T$가 관측될 확률 $p(O|\theta)$를 계산하는 것이다. 먼저, 첫 번째 observation $o_1$이 나타날 확률은 [식 1]과 같이 계산된다.

그다음, 첫 번째와 두 번째 observation이 연속으로 나타날 확률은 다음과 같다.

따라서, 시간 $T$까지의 observation $O = o_1, o_2, ..., o_T$가 나타날 확률은 [식 3]과 같다.

그러나 [식 3]을 계산하는 것은 $O(2TN^T)$의 막대한 time complexity가 요구된다. 이를 해결하기 위해 HMM은 dynamic programming 기반의 $O(TN^2)$의 time complexity를 갖는 forward algorithm을 이용한다. Forward algorithm에서는 새로운 변수인 $\alpha_t(q_j)$를 아래와 같이 정의한다.

또한, $\alpha_t(q_j)$는 아래와 같이 재귀적인 형태로 계산할 수 있다.

아래의 [알고리즘 1]은 HMM에서 forward algorithm을 이용하여 [식 3]의 likelihood를 계산하는 과정을 나타낸다.

위의 [그림 3]의 예제에서 지출내역이 1, 3, 2, 1, 2인 ($O$ = 1, 3, 2, 1, 2) 경우, forward algorithm을 이용한 likelihood는 0.00134349로 계산된다.

2.2. 주어진 observation이 나타날 확률이 가장 큰 state 계산: Viterbi algorithm

두 번째 문제는 주어진 observation이 나타날 확률이 가장 큰 state의 연속 $S^{*} = s_{1}^{*} s_{2}^{*} ... s_{T}^{*}$를 찾는 것이다. 이러한 과정을 decoding이라고 한다. HMM에서는 앞의 forward algorithm과 유사하게 dynamic programming 기반의 Viterbi algorithm을 이용하여 최적의 state를 찾는다. 아래의 [알고리즘 2]는 viterbi algorithm의 동작을 보여준다.

 

위의 [그림 3]의 예제에서 지출내역이 1, 3, 2, 1, 2인 ($O$ = 1, 3, 2, 1, 2) 경우, Viterbi algorithm을 이용하여 찾은 최적의 state는 study, friend, game, study, game이 된다. 따라서, 우리는 과거의 지출내역이 1, 3, 2, 1, 2인 경우, 가장 높은 확률로 과거 5일동안 공부, 친구 만나기, 게임, 공부, 게임를 했었다고 생각할 수 있다.

2.3. HMM의 parameter 학습: Baum-Welch algorithm

HMM의 parameter 학습은 observation들의 집합인 $\boldsymbol{O} = \{O^{(1)}, O^{(2)}, ..., O^{(K)} \}$로부터 최적의 parameter $\theta^{*} = \{ \pi^{*}, \boldsymbol{A}^{*}, \boldsymbol{B}^{*} \}$를 추정하는 것이다.

HMM의 parameter 학습에는 주로 EM algorithm의 한 종류인 Baum-Welch algorithm가 이용된다. 이 알고리즘에서는 먼저 $\boldsymbol{O}$에 포함된 observation들이 나타날 확률을 의미하는 likelihood $p(\boldsymbol{O}, \boldsymbol{S}|\theta)$를 정의한다. 여기에서 $\boldsymbol{S}$는 $\boldsymbol{O}$에 포함된 각 observation에 대해 은닉된 state가 어떻게 변화하였는지를 나타낸다. 만약 $\boldsymbol{S}$를 정확히 알고 있다면, $p(\boldsymbol{O}, \boldsymbol{S}|\theta)$는 아래와 같이 계산된다.

양변에 log를 취하면 [식 7]과 같다.

그러나 대부분의 경우에는 $\boldsymbol{O}$에 대한 $\boldsymbol{S}$를 모르기 때문에 아래와 같이 log-likelihood를 변형하여 $Q(\theta, \theta^{'})$를 정의한다. [식 8]에서 $\theta$는 현재의 parameter, $\theta^{'}$는 이전의 parameter를 의미한다. 왜 이전의 parameter를 고려하여 식을 정의하는지를 비롯하여 Baum-Welch algorithm이 왜 다음과 같이 전개되는 지를 알기 위해서는 EM algorithm에 대한 이해가 필요하다.

[식 7]을 [식 8]에 대입하면, Baum-Welch algorithm을 통해 최대화하고자 하는 $Q(\theta, \theta^{'})$는 다음과 같다.

마지막으로, 라그랑주 승수법 (Lagrange multiplier method)를 이용하여 확률의 정의에 의한 제약 조건을 $Q(\theta, \theta^{'})$에 추가하면, 최종 목적 함수 $L(\theta, \theta^{'})$는 [식 10]과 같이 주어진다.

따라서, HMM의 학습은 $L(\theta, \theta^{'})$를 최대화하는 $\theta^{*} = \{\pi^{*}, \boldsymbol{A}^{*}, \boldsymbol{B}^{*} \}$를 찾는 것과 같다. $L(\theta, \theta^{'})$을 최대화하는 각각의 parameter들은 아래와 같이 계산된다. 여기에서 $\pi_{i} = p(q_i), A_{ij} = p(q_j|q_i), B_{ij} = p(y_j|q_i)$를 의미한다.

 

그다음, $A_{ij}$는 [식 12]와 같이 계산된다.

 

 

마지막으로, $B_{ij}$는 [식 13]과 같이 계산된다.