선형회귀는 입력 $\textbf{x} \in \mathbb{R}^{d \times 1}$와 출력 $y \in \mathbb{R}$를 식 (1)과 같은 선형 관계로 모델링하기 위한 회귀분석이다.
$$\begin{equation} y = \textbf{w}_1 \textbf{x}_1 + ... \textbf{w}_d \textbf{x}_d + b = \textbf{w}^T \textbf{x} + b \tag{1} \end{equation}$$
위의 식에서 $\textbf{w} \in \mathbb{R}^{d \times 1}$와 $b \in \mathbb{R}$는 선형회귀 모델의 매개변수이다.

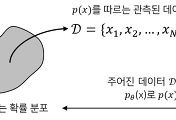
$N$개의 데이터를 포함하는 데이터셋 $\mathcal{D} = \{(\textbf{x}^{(1)}, y^{(1)}), ..., (\textbf{x}^{(N)}, y^{(N)}) \}$에 대해 선형회귀 모델은 그림 1과 같이 각 데이터에 대한 오차 (error)를 최소화하도록 학습된다. 모델 학습에서 평균 제곱 오차 (Mean squared error, MSE)를 손실 함수 (loss function)로 이용할 경우 선형회귀 모델의 학습은 아래의 식 (2)로 정의된다.
$$\begin{equation} \theta^* = \underset{\theta}{\text{argmin}} \; \frac{1}{N} \sum_{i=1}^N \left(\textbf{w}^T\textbf{x}^{(i)} + b - y^{(i)} \right)^2 \tag{2} \end{equation}$$
식 (2)에서 $\theta = \{\textbf{w}, b\}$는 선형회귀 모델의 매개변수이다. 머신러닝에서는 일반적으로 모델의 최적 매개변수를 경사하강법 (gradient descent method)으로 찾지만, 선형회귀 모델은 특수한 경우로써 최적 매개변수를 찾기 위한 analytic solution이 존재한다. [link]
최대 우도 추정은 이전글에서 설명한 바와 같이 likelihood $p(\mathcal{D}|\theta)$를 최대화하여 최적 매개변수 $\theta^*$를 찾는 방법이다. MLE의 관점에서 선형회귀를 서술하기 위해 먼저 선형회귀 모델의 출력 변수 $y$를 식 (3)과 같은 확률변수로 정의한다.
$$\begin{equation} y^{(i)} = \textbf{w}^T \textbf{x}^{(i)} + b + \epsilon^{(i)} \tag{3} \end{equation}$$
위의 식에서 $i$번째 예측에 대한 오차 $\epsilon^{(i)}$는 정규 분포 $\mathcal{N}(0, \sigma^2)$를 따른다고 가정하며, $\sigma > 0$는 어떠한 상수 또는 학습 가능한 매개변수로 설정될 수 있다. 추가적으로 출력 변수 $y$를 독립항등분포 확률변수 (i.i.d. random variable)라고 가정하면, 선형회귀 모델의 MLE 기반 학습은 아래의 식 (4)와 같이 서술된다.
$$\begin{align*} \theta^*, \sigma^* = \; &\underset{\theta, \sigma}{\text{argmax}} \; \log p(\mathcal{D}|\theta)\\ = \; &\underset{\theta, \sigma}{\text{argmax}} \; \log \prod_{i=1}^N p(y^{(i)}|\textbf{x}^{(i)};\theta) \\ = \; &\underset{\theta, \sigma}{\text{argmax}} \; \sum_{i=1}^N \log p(y^{(i)}|\textbf{x}^{(i)};\theta)\\ = \; &\underset{\theta , \sigma }{\text{argmax}} \; \sum_{i=1}^N \log \mathcal{N}(y^{(n)}|\textbf{w}^T \textbf{x}^{(i)} + b, \sigma^2)\\ = \; &\underset{\theta , \sigma}{\text{argmax}} \; \sum_{i=1}^N \left\{ -\frac{1}{2} \log(2\pi) -\log \sigma - \frac{(\textbf{w}^T \textbf{x}^{(i)} + b - y^{(i)})^2}{2\sigma^2} \right\}\\ = \; &\underset{\theta , \sigma}{\text{argmax}} \; - N\log \sigma - \frac{1}{2\sigma^2} \sum_{i=1}^N (\textbf{w}^T \textbf{x}^{(i)} + b - y^{(i)})^2\\ = \; &\underset{\theta , \sigma}{\text{argmin}} \; N\log \sigma + \frac{1}{2\sigma^2} \sum_{i=1}^N (\textbf{w}^T \textbf{x}^{(i)} + b - y^{(i)})^2 \tag{4} \end{align*}$$
만약 $\sigma$를 어떠한 상수로 가정하면 $\sigma$는 최적화 과정의 변수가 아니게 되며, 아래의 식 (5)를 얻는다.
$$\begin{equation} \theta^* = \; \underset{\theta}{\text{argmin}} \; \frac{1}{N} \sum_{i=1}^N (\textbf{w}^T \textbf{x}^{(i)} + b - y^{(i)})^2 \tag{5} \end{equation}$$
따라서, 식 (2)의 평균 제곱 오차 기반 선형회귀 모델의 학습은 오차 $\epsilon$의 평균이 0이고 표준편차가 어떠한 상수로 가정했을 때의 MLE와 같다.
MLE를 기반으로 하는 식 (2)와 (4)의 매개변수 최적화는 매개변수의 분포를 단순한 균등분포 (uniform distribution)로 가정한 것과 같다.[link] 이 항목에서는 단순한 균등분포를 넘어 모델 매개변수에 대해 우리의 사전지식을 적용할 수 있는 베이지안 선형회귀에 대해 서술한다.
베이지안 선형회귀에서도 아래의 식 (6)과 같이 예측에 대한 오차를 포함하여 입력과 출력의 선형 관계를 가정한다. 아래의 식에서 $\epsilon^{(i)} \sim \mathcal{N}(0, \sigma^2)$는 $i$번째 데이터에 대한 예측 오차이다.
$$\begin{equation} y^{(i)} = \textbf{w}^T \textbf{x}^{(i)} + b + \epsilon^{(i)} \tag{6} \end{equation}$$
베이지안 선형회귀에서는 모델 매개변수가 어떠한 상수일 것이라는 가정의 MLE가 아니라, 모델 매개변수의 분포를 가정하는 MAP (maximum a posteriori)를 바탕으로 모델 매개변수 $\theta$를 최적화한다. MLE와 MAP의 자세한 차이점은 이전글에서 설명했다. MAP에서는 아래의 식 (7)과 같이 사후 확률 (posterior probability) $p(\theta|\mathcal{D})$를 최대화함으로써 모델 매개변수 $\theta$를 최적화한다.
$$\begin{equation} \theta^* = \; \underset{\theta}{\text{argmax}} \; p(\theta|\mathcal{D}) \tag{7} \end{equation}$$
베이즈 정리에 의해 식 (7)의 목적 함수는 아래와 같이 가능도 (likelihood) $p(\mathcal{D}|\theta)$와 사전 확률 (prior probability) $p(\theta)$로 나누어진다.
$$\begin{align*} \theta^* &= \; \underset{\theta}{\text{argmax}} \; p(\theta|\mathcal{D})\\ &= \; \underset{\theta}{\text{argmax}} \; \frac{p(\mathcal{D}|\theta)p(\theta)}{p(\mathcal{D})}\\ &= \; \underset{\theta}{\text{argmax}} \; p(\mathcal{D}|\theta) p(\theta)\\ &= \; \underset{\theta}{\text{argmax}} \; \log p(\mathcal{D}|\theta) + \log p(\theta) \tag{8} \end{align*}$$
식 (4)의 MLE 기반 방법론에서는 사전 확률 $p(\theta)$를 상수로 가정하고, 가능도에 해당하는 $p(\mathcal{D}|\theta)$만을 고려하여 매개변수를 최적화했었다. 그러나 베이지안 선형회귀에서는 사전 확률 $p(\theta)$까지 고려하여 매개변수를 최적화한다. 일반적으로 MAP에서 매개변수에 대한 사전 확률 $p(\theta)$는 데이터 또는 직관에 의해 설정되며, $p(\theta)$의 설정은 학습된 모델의 예측 정확도에 영향을 줄 수 있다.
3-1. 사전 확률을 정규 분포로 가정한 경우
사전 확률 $p(\theta)$를 정규 분포 $\mathcal{N}(\boldsymbol{\mu}, \textbf{S})$로 정의할 수 있으며, 머신러닝에서는 일반적으로 $p(\theta)$를 $\mathcal{N}(0, \textbf{I})$로 가정한다. 사전 확률에 대한 이러한 가정에서 선형회귀 모델의 매개변수는 아래와 같이 계산된다.
$$\begin{align*} \theta^*, \sigma^* &= \; \underset{\theta, \sigma}{\text{argmax}} \; \log p(\mathcal{D}|\theta) + \log p(\theta)\\ &= \; \underset{\theta}{\text{argmin}} \; \frac{1}{2\sigma^2} \sum_{i=1}^N (\textbf{w}^T \textbf{x}^{(i)} + b - y^{(i)})^2 + \frac{1}{2} ||\theta||_2^2 \tag{9} \end{align*}$$
따라서, 사전 확률을 $p(\theta) = \mathcal{N}(\theta | 0, \textbf{I})$로 가정한 경우에는 평균 제곱 오차와 모델 매개변수의 크기를 동시에 줄이도록 모델이 학습된다. 이는 모델 매개변수에 $L_2$ 제약을 주는 ridge regression과 같다.
3-2. 사전 확률을 라플라스 분포로 가정한 경우
사전 확률을 정규 분포가 아니라 라플라스 분포 $\text{Laplace}(0, \textbf{I})$로 가정한 경우에는 아래의 식 (10)과 같이 모델 매개변수가 계산된다.
$$\begin{equation} \theta^*, \sigma^* = \; \underset{\theta, \sigma}{\text{argmin}} \; \frac{1}{2\sigma^2} \sum_{i=1}^N (\textbf{w}^T \textbf{x}^{(i)} + b - y^{(i)})^2 + \frac{1}{2}||\theta|| \tag{10} \end{equation}$$
식 (10)에 의해 만들어지는 모델은 $L_1$ 제약이 추가된 선형회귀 모델인 LASSO와 같다.
이 글에서는 베이지안 선형회귀가 매개변수의 크기에 대한 제약이 추가된 선형회귀임을 보였다. 다음글에서는 매개변수의 크기에 대한 제약이 왜 모델의 예측 정확도 향상에 도움이 되는지를 이론적으로 설명할 것이다.
'머신러닝 > 확률모델' 카테고리의 다른 글
| 몬테카를로 방법 (Monte Carlo Method)과 베이지안 머신러닝 (3) | 2024.01.07 |
|---|---|
| [머신러닝] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)과 EM 알고리즘 (21) | 2023.12.29 |
| Reparameterization Trick에 대한 수학적 이해와 기댓값의 미분가능성 (2) | 2023.12.21 |
| Conjugate Prior의 정의와 예제 (0) | 2023.12.18 |
| 확률에 대한 Frequentist와 Bayesian 접근, 그리고 MLE와 MAP (0) | 2023.12.05 |