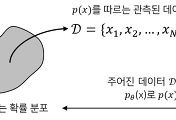
베이지안 머신러닝 (Bayesian machine learning)에서는 주어진 데이터셋 $\mathcal{D}$에 대해 모델 매개변수 $\theta$의 사후 확률 (posterior probability) $p(\theta|\mathcal{D})$를 최대화하도록 모델 학습이 진행된다. 이를 식으로 나타내면 아래와 같다.
$$\begin{align*} \theta^* &= \underset{\theta}{\text{argmax}} \; p(\theta|\mathcal{D})\\ &= \underset{\theta}{\text{argmax}} \; p(\mathcal{D}|\theta) p(\theta) \tag{1} \end{align*}$$
Conjugate prior는 식 (1)의 베이지안 머신러닝에서 사전 확률 $p(\theta)$가 어떠한 특정 조건을 만족하는 경우를 의미하는 것으로써, 아래와 같이 정의된다.
요약하자면, 사전 분포 $p(\theta)$와 사후 분포 $p(\theta|\mathcal{D})$가 같은 확률 분포의 형태를 가질 경우 $p(\theta)$를 conjugate prior라고 한다. 더 정확히는 $p(\theta)$를 가능도 (likelihood) $p(\mathcal{D}|\theta)$에 대한 conjugate prior라고 한다.
Conjugate prior의 가장 큰 장점은 최대 사후 확률 추정 (maximum a posteriori estimation)을 포함한 베이지안 학습 과정에 대한 수학적 전개가 매우 단순해지는 것이다. 또한 conjugate prior를 이용하면 우리가 최종적으로 계산해야하는 사후 확률을 우리가 이미 알고 있는 형태 또는 복잡도가 낮은 함수로 계산할 수 있다. 베이지안 머신러닝의 가장 큰 단점이 사후 확률에 대한 계산이 복잡하고 많은 계산량이 요구된다는 점인데, conjugate prior를 이용하면 이러한 문제를 어느정도 완화시킬 수 있는 것이다.

그러나 가능도가 정규 분포와 같이 exponential family에 속하면 conjugate prior를 갖지만,[proof] 모든 가능도에 대해 conjugate prior가 존재하는 것은 아니다. 베이지안 통계학에서 많이 이용되는 가능도와 사전 분포의 쌍, 그리고 그에 따른 사후 분포는 아래와 같다.
| 가능도 $p(\mathcal{D}|\theta)$ | 사전 분포 $p(\theta)$ | 사후 분포 $p(\theta|\mathcal{D})$ |
| 베르누이 분포 | 베타 분포 | 베타 분포 |
| 이항 분포 | 베타 분포 | 베타 분포 |
| 정규 분포 | 정규 분포 | 정규 분포 |
| 다항 분포 | Dirichlet 분포 | Dirichlet 분포 |
한 가지 착각하기 쉬운 것은 exponential family에 속하지 않는다고 conjugate prior가 존재하지 않는 것은 아니다. 반례로써 균등 분포 (uniform distribution)는 exponential family에 속하지 않지만 conjugate prior를 갖는다. 아래의 내용은 몇 가지 conjugate prior 예시에 대해 주어진 가능도와 사전 분포에 따라 어떻게 사후 분포의 형태가 결정되는지를 서술한 것이다.
예시 1. 가능도가 이항 분포, 사전 분포가 베타 분포인 경우
가능도가 $p(x|\theta) = B(x; N, \theta)$이고 사전 분포가 $p(\theta) = Beta(\theta; \alpha, \beta)$이면, 사후 분포 $p(\theta|x)$는 아래와 같다.
$$\begin{align*} p(\theta|x) &\propto p(x|\theta) p(\theta)\\ &\propto \binom{N}{x} \theta^x (1 - \theta)^{N - x} \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} \theta^{\alpha - 1} (1 - \theta)^{\beta - 1}\\ &\propto \theta^{(x + \alpha) - 1} (1 - \theta)^{(N - x + \beta) - 1}\\ &\propto Beta(x + \alpha, N - x + \beta) \tag{2} \end{align*}$$
따라서, 사후 분포 $p(\theta|x)$는 사전 분포 $p(\theta)$와 같은 베타 분포로 정의된다.
예시 2. 가능도와 사전 분포가 정규 분포인 경우
공분산 행렬 $\Sigma$를 알고 있다는 가정 하에 가능도가 $p(\textbf{x}|\theta) = \mathcal{N}(\textbf{x}; \boldsymbol{\mu}, \Sigma)$이고 매개변수인 $\boldsymbol{\mu}$에 대한 사전 분포가 $p(\boldsymbol{\mu}) = \mathcal{N}(\boldsymbol{\mu}; \boldsymbol{\mu}_0, \Sigma_0)$이면, 사후 분포 $p(\boldsymbol{\mu}|\textbf{x})$는 아래와 같다.
$$\begin{align*} p(\theta|\textbf{x}) &\propto p(\textbf{x}|\theta) p(\theta)\\ &\propto \exp \left(-\frac{1}{2}(\textbf{x} - \boldsymbol{\mu})^T\Sigma^{-1}(\textbf{x} - \boldsymbol{\mu}) \right) \exp \left(-\frac{1}{2} (\boldsymbol{\mu} - \boldsymbol{\mu}_0)^T \Sigma_0^{-1} (\boldsymbol{\mu} - \boldsymbol{\mu}_0) \right) \tag{3} \end{align*}$$
식 (3)의 지수 함수의 내부는 아래와 같이 정리된다.
$$\begin{align*} &-\frac{1}{2} \left(\textbf{x}^T \Sigma^{-1} \textbf{x} + \boldsymbol{\mu}^T \Sigma^{-1} \boldsymbol{\mu} - 2\textbf{x}^T\Sigma^{-1}\boldsymbol{\mu} + \boldsymbol{\mu}^T \Sigma_0^{-1} \boldsymbol{\mu} + \boldsymbol{\mu}_0^T \Sigma_0^{-1} \boldsymbol{\mu}_0 - 2\boldsymbol{\mu}_0^T \Sigma_0^{-1} \boldsymbol{\mu}_0 \right)\\ &= \boldsymbol{\mu}^T(\Sigma^{-1} + \Sigma_0^{-1}) \boldsymbol{\mu} - 2\boldsymbol{\mu}^T (\Sigma^{-1} \textbf{x} + \Sigma_0^{-1} \boldsymbol{\mu}_0) + \textbf{x}^T\Sigma^{-1}\textbf{x} + \boldsymbol{\mu}_0^T \Sigma_0^{-1} \boldsymbol{\mu}_0 \tag{4} \end{align*}$$
식 (4)의 요소들을 아래와 같이 정의한다.
$$\begin{equation} \textbf{M} = \Sigma^{-1} + \Sigma_0^{-1} \tag{5} \end{equation}$$
$$\begin{equation} \textbf{b} = \Sigma^{-1}\textbf{x} + \Sigma_0^{-1} \boldsymbol{\mu}_0 \tag{6} \end{equation}$$
완전제곱식 연산에 의해 식 (4)는 아래와 같이 변형된다
$$\begin{align*} &\boldsymbol{\mu}^T \textbf{M} \boldsymbol{\mu} - 2 \textbf{b}^T \boldsymbol{\mu} + \textbf{x}^T \Sigma^{-1} \textbf{x} + \boldsymbol{\mu}_0^T \Sigma_0^{-1} \boldsymbol{\mu}_0\\ &= (\boldsymbol{\mu} - \textbf{M}^{-1} \textbf{b})^T \textbf{M} (\boldsymbol{\mu} - \textbf{M}^{-1} \textbf{b}) - \textbf{b}^T \textbf{M}^{-1} \textbf{b} + \textbf{x}^T\Sigma^{-1}\textbf{x} + \boldsymbol{\mu}_0^T \Sigma_0^{-1} \boldsymbol{\mu}_0 \tag{7} \end{align*}$$
따라서, 사후 분포는 아래와 같이 나타낼 수 있다.
$$\begin{align*} p(\boldsymbol{\mu}|\textbf{x}) &\propto \exp \left(-\frac{1}{2} \left\{ (\boldsymbol{\mu} - \textbf{M}^{-1} \textbf{b})^T \textbf{M} (\boldsymbol{\mu} - \textbf{M}^{-1} \textbf{b}) - \textbf{b}^T \textbf{M}^{-1} \textbf{b} \right\} \right)\\ &\propto \mathcal{N}(\boldsymbol{\mu}; \textbf{M}^{-1}\textbf{b}, \textbf{M}^{-1}) \tag{8} \end{align*}$$
앞에서 말한 바와 같이 모든 가능도에 대해 conjugate prior가 존재하는 것은 아니다. 따라서 일반화된 문제에 대해 베이지안 통계를 적용하기 위해서는 conjugate prior가 존재하지 않는 경우에 대한 방법이 필요하다. 가장 많이 사용되는 방법은 샘플링을 통한 함수 근사화 기법인 몬테카를로 방법 (Monte Carlo method)이다. 다음글에서는 몬테카를로 방법에 대해 소개하고, 이를 어떻게 베이지안 머신러닝에 적용할 수 있는지를 설명한다.
'머신러닝 > 확률모델' 카테고리의 다른 글
| 몬테카를로 방법 (Monte Carlo Method)과 베이지안 머신러닝 (3) | 2024.01.07 |
|---|---|
| [머신러닝] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)과 EM 알고리즘 (21) | 2023.12.29 |
| Reparameterization Trick에 대한 수학적 이해와 기댓값의 미분가능성 (2) | 2023.12.21 |
| 선형회귀 (Linear Regression)에 대한 여러 접근법 (0) | 2023.12.09 |
| 확률에 대한 Frequentist와 Bayesian 접근, 그리고 MLE와 MAP (0) | 2023.12.05 |