어떠한 학습 문제에서 아래와 같은 두 학생 A와 B를 생각해볼 수 있다.
- 학생 A: 고집이 너무 강해서 아무리 새로운 지식을 학습을 시켜도 자신의 주관대로 판단하는 성격
- 학생 B: 귀가 너무 얇아서 옳은 것이든 틀린 것이든 학습시키는 그대로 수용하는 성격
위의 예시를 머신러닝 문제에서 생각해보면 A는 편향이 크고 분산은 작은 예측 모델이며, 대표적으로 선형회귀 (linear regression)와 같은 모델이 있다. 반면에 B는 편향은 작지만 분산이 큰 예측 모델이며, 대표적으로 고차 다항 회귀 (high-degree polynomial regression)나 심층 인공신경망 (deep neural network) 등이 있다.
선형회귀와 같이 편향이 크고 분산은 작은 모델은 그림 1a의 예측 모델 $g(\textbf{x};\theta)$처럼 새로운 학습 데이터가 주어지더라도 학습이 충분히 되지 않은 underfitting 상태에 존재할 가능성이 높다. 반대로 심층 인공신경망과 같이 편향은 작지만 분산이 큰 모델은 그림 1c의 예측 모델 $h(\textbf{x};\theta)$처럼 주어진 학습 데이터를 너무 과하게 수용하여 overfitting이 발생할 가능성이 높다.
편향이 큰 예측 모델 A는 새로운 학습 데이터가 주어지더라도 학습이 충분히 되지 않은 underfitting 상태의 모델이며, 그림1a의 예측 모델 $g(\textbf{x};\theta)$이다. 분산이 큰 예측 모델 B는 주어진 학습 데이터를 너무 과하게 수용하여 overfitting이 발생한 모델이며, 그림 1c의 예측 모델 $h(\textbf{x};\theta)$이다.

머신러닝에서 우리의 목표는 그림 1b의 $q(\textbf{x};\theta)$와 같이 편향과 분산이 적절하게 최소화된 예측 모델을 만드는 것이다. 그러나 일반적으로 편향과 분산은 동시에 최소화될 수 없는데, 이러한 현상을 편향-분산 트레이드오프 (bias-variance tradeoff)라고 한다.
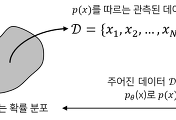
모델 학습에서 우리의 목표는 주어진 데이터셋 $\mathcal{D} = \{(\textbf{x}_1, y_1), ..., (\textbf{x}_N, y_N)\}$에 대해 입력 $\textbf{x}_n$과 출력 $y_n$의 관계를 오차 없이 표현하는 어떠한 함수 $f^*$를 찾는 것이다. 출력 변수 $y$는 함수의 출력 $f^*(\textbf{x})$와 노이즈 $\epsilon$을 기반으로 아래의 식 (1)과 같이 정의할 수 있다.
$$\begin{equation} y = f^*(\textbf{x}) + \epsilon \tag{1} \end{equation}$$
노이즈 $\epsilon$은 정규 분포 $\mathcal{N}(0, \sigma^2)$을 따른다고 가정한다. 예측 모델 $f$에 대한 예측 오차의 기댓값은 식 (2)와 같이 정의할 수 있으며, 머신러닝의 목적은 식 (2)의 기댓값을 최소화하는 예측 모델을 찾는 것이다.
$$\begin{equation} \text{Loss} = \text{E}[(y - f(\textbf{x}))^2] \tag{2} \end{equation}$$
먼저, 편향-분산 트레이드오프를 유도하기 위해 $\text{E}[X^2]$은 아래의 과정을 통해 분해된다는 것을 보인다.
$$\begin{align*} \text{E}[X^2] &= \text{E}[X^2] - \text{E}[2X\text{E}[X]] + \text{E}[2X\text{E}[X]] - \text{E}[\text{E}[X]^2] + \text{E}[\text{E}[X]^2]\\ &= \text{E}[X^2 - 2X\text{E}[X] + \text{E}[X]^2] + 2\text{E}[X]^2 - \text{E}[X]^2\\ &= \text{E}[(X - \text{E}[X])^2] + \text{E}[X]^2\\ &= \text{Var}[X] + \text{E}[X]^2 \tag{3} \end{align*}$$
식 (3)을 기반으로 식 (2)의 기댓값은 아래와 같이 변형된다.
$$\begin{align*} \text{E}[(y - f(\textbf{x}))^2] &= \text{E}[y^2 + f(\textbf{x})^2 - 2yf(\textbf{x})]\\ &= \text{E}[y^2] + \text{E}[f(\textbf{x})^2] - 2\text{E}[yf(\textbf{x})]\\ &= \text{Var}[y] + \text{E}[y]^2 + \text{Var}[f(\textbf{x})] + \text{E}[f(\textbf{x})]^2 - 2\text{E}[yf(\textbf{x})]\\ &= \text{Var}[y] + \text{Var}[f(\textbf{x})] + \text{E}[y]^2 + \text{E}[f(\textbf{x})]^2 - 2\text{E}[y]\text{E}[f(\textbf{x})]\\ &= \text{Var}[y] + \text{Var}[f(\textbf{x})] + (\text{E}[y] - \text{E}[f(\textbf{x})])^2\\ &= \text{Var}[y] + \text{Var}[f(\textbf{x})] + (\text{E}[f^*(\textbf{x}) - f(\textbf{x})] + \text{E}[\epsilon])^2\\ &= \text{Var}[y] + \text{Var}[f(\textbf{x})] + (\text{E}[f^*(\textbf{x}) - f(\textbf{x})])^2 \tag{4} \end{align*}$$
위의 식에서 출력 변수 $y$의 분산 $\text{Var}[y]$는 노이즈 $\epsilon$이 정규 분포 $\mathcal{N}(0, \sigma^2)$을 따른다는 가정을 바탕으로 아래와 같이 계산된다.
$$\begin{align*} \text{Var}[y] &= \text{E}[(y - \text{E}[y])^2]\\ &= \text{E}[(f^*(\textbf{x}) + \epsilon - f^*(\textbf{x}))^2]\\ &= \text{E}[\epsilon^2]\\ &= \text{Var}[\epsilon] + \text{E}[\epsilon]\\ &= \sigma^2 \tag{5} \end{align*}$$
따라서, 식 (2)의 기댓값은 아래의 식 (6)과 같이 노이즈 $\epsilon$의 분산과 예측모델 $f$에 대한 편향 및 분산으로 분해된다.
$$\begin{equation} \text{E}[(y - f(\textbf{x}))^2] = \sigma^2 + (\underbrace{\text{E}[f^*(\textbf{x}) - f(\textbf{x})]}_{= \; \text{bias of} \; f})^2 + \underbrace{\text{Var}[f(\textbf{x})]}_{= \; \text{variance of} \; f} \tag{6} \end{equation}$$
식 (6)에서 $\sigma^2$는 노이즈의 분산으로써 예측 모델 $f$와 독립적인 어떠한 상수로 존재하는 예측 오차이다. 결과적으로 예측 오차를 최소화하기 위해서는 편향의 제곱과 분산에 관한 항을 최소화해야한다. 그러나 식 (6)에서 보이듯이 편향과 분산 사이에는 트레이드오프가 존재한다.
만약 편향에 관한 항을 최소화힉 위해 $f(\textbf{x}) = f^*(\textbf{x})$가 되도록 모델을 학습시키면, 편향은 0이 되겠지만 모델은 모든 입력과 출력 변수의 관계를 표현할만큼 복잡해야하기 때문에 분산이 증가할 것이다. 반대로 분산에 관한 항을 최소화하기 위해 예측 모델이 항상 어떠한 상수만을 출력하도록 학습시키면, 분산은 0이 되겠지만 모델의 출력과 $f^*(\textbf{x})$ 사이의 차이가 커져서 편향은 증가할 것이다.
머신러닝에서 가중치 규제는 모델의 학습에서 모델 매개변수 $\theta$의 크기가 작아지도록 학습의 제약 조건을 주는 것을 말한다. 가장 대표적인 방법으로는 $||\theta||_2^2$로 정의되는 $L_2$ 규제 ($L_2$ regularization)가 있으며, $L_2$ 규제를 적용할 경우에는 식 (7)과 같이 모델이 학습된다. $L(\mathcal{D};\theta)$는 주어진 데이터셋 $\mathcal{D}$에 대한 모델의 예측 오차이다.
$$\begin{equation} \theta^* = \underset{\theta}{\text{argmin}} \; L(\mathcal{D};\theta) + ||\theta||_2^2 \tag{7} \end{equation}$$
이전글에서 maximum a posteriri (MAP) 기반의 모델 학습에서 매개변수의 사전 확률 $p(\theta)$는 가중치 규제 항으로 변환될 수 있음을 설명했다. 이러한 결과에 더하여 적절한 사전 분포를 설정할 경우 MAP 기반의 모델 학습이 단순히 예측 오차 $L(\mathcal{D};\theta)$만을 최소화하는 것보다 효과적임을 보였다.
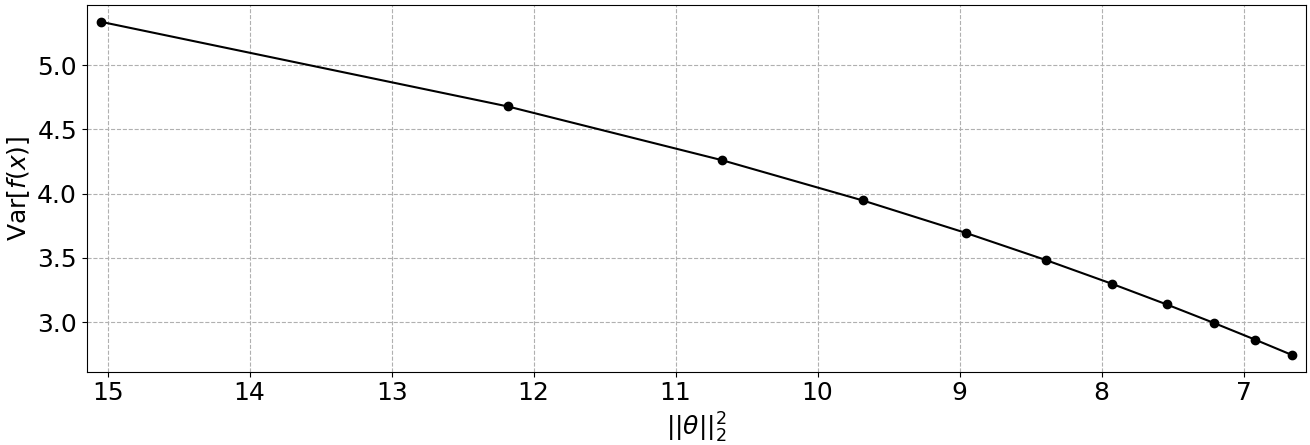
가중치 규제의 효과는 MAP 이외에도 식 (6)에서 설명하였던 편향-분산 트레이드오프의 관점에서도 해석할 수 있다. 위의 그림 2는 매개변수의 크기 $||\theta||_2^2$에 따른 모델 분산 $\text{Var}[f(\textbf{x})]$을 측정한 것이며, $||\theta||_2^2$가 감소할수록 $\text{Var}[f(\textbf{x})]$도 감소하였다. 따라서 식 (7)과 같이 가중치 규제를 추가한 모델의 학습은 가능한 범위 내에서 편향과 분산을 동시에 최소화할 수 있는 모델을 찾는 것과 같으며, 이를 통해 예측 오차의 기댓값이 더 낮은 모델을 생성할 수 있다.
'머신러닝 > 확률모델' 카테고리의 다른 글
| Unbiased and Biased Estimators의 개념과 머신러닝 (1) | 2024.01.11 |
|---|---|
| 몬테카를로 방법 (Monte Carlo Method)과 베이지안 머신러닝 (4) | 2024.01.07 |
| [머신러닝] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)과 EM 알고리즘 (18) | 2023.12.29 |
| Reparameterization Trick에 대한 수학적 이해와 기댓값의 미분가능성 (2) | 2023.12.21 |
| Conjugate Prior의 정의와 예제 (0) | 2023.12.18 |