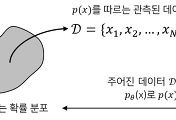
Gaussian Mixture Model (GMM)은 이름 그대로 가우시안 분포 (정규분포)를 여러 개 혼합하여 데이터의 복잡한 분포를 근사하기 위한 머신러닝 알고리즘이다. GMM은 그림 1과 같이 $K$개의 가우시안 분포를 혼합하여 복잡한 형태의 확률분포를 근사한다. $K$는 몇 개의 가우시안 분포를 혼합할 것인지를 결정하는 GMM의 hyperparameter이며, 그림 1은 $K=3$으로 설정된 GMM을 나타낸다.

GMM에서 주어진 데이터 $\textbf{x}$가 발생할 확률은 아래의 식 $\eqref{eq:gmm}$과 같이 $K$개의 가우시안 확률밀도함수 (probability density function)의 혼합으로 정의된다.
$$\begin{equation} p(\textbf{x}) = \sum_{k=1}^K \pi_k \mathcal{N}(\textbf{x} ; \boldsymbol{\mu}_k, \Sigma_k) \label{eq:gmm}\end{equation}$$
식 $\eqref{eq:gmm}$에서 $\pi_k \in [0, 1]$는 mixing coefficient라고 하며, 혼합 분포에 대한 확률밀도함수에서 $k$번째 가우시안 분포가 선택될 확률을 의미한다. 따라서 $\pi_k$는 아래의 반드시 조건을 만족해야한다.
$$\begin{equation} 0 \leq \pi_k \leq 1 \; \text{and} \; \sum_{k=1}^K \pi_k = 1 \label{eq:const_pi} \end{equation}$$
GMM을 학습시킨다는 것은 주어진 데이터셋 $\mathcal{X} = \{\textbf{x}_1, \textbf{x}_2, ..., \textbf{x}_N\}$에 대하여 데이터의 확률 $p(\textbf{x})$를 최대화하는 매개변수 $\theta = \{\pi_1, ..., \pi_K, \boldsymbol{\mu}_1, ..., \boldsymbol{\mu}_K, \Sigma_1, ..., \Sigma_K \}$를 추정하는 것과 같다.
최대 우도 추정 (MLE)은 확률모델의 매개변수를 최적화하기 위해 머신러닝에서 가장 일반적으로 이용되는 방법 중 하나이다. 각 데이터가 동일한 확률 분포에서 다른 데이터와 독립적으로 생성되었다고 가정하면 (i.i.d. 가정 참고), 주어진 데이터 $\mathcal{X} = \{\textbf{x}_1, \textbf{x}_2, ..., \textbf{x}_N\}$에 대한 로그-가능도 (log-likelihood)는 아래와 같이 정의된다.
$$\begin{equation} L(\mathcal{X}; \theta) = \log p(\mathcal{X};\theta) = \log \prod_{n=1}^N p(\textbf{x}_n;\theta) \label{eq:log_likelihood} \end{equation}$$
MLE는 식 $\eqref{eq:log_likelihood}$을 최대화하도록 모델을 학습시킨다. GMM에서는 식 $\eqref{eq:gmm}$과 같이 데이터의 분포 $p(\textbf{x})$를 $K$개 가우시안 분포의 혼합으로 가정하였으므로, GMM의 학습을 위해 최대화해야하는 로그-가능도는 최종적으로 아래의 식 $\eqref{eq:log_likelihood_gmm}$와 같다.
$$\begin{equation} L(\mathcal{X};\theta) = \sum_{n=1}^N \log \left( \sum_{k=1}^K \pi_k \mathcal{N}(\textbf{x}_n; \boldsymbol{\mu}_k, \Sigma_k) \right) \label{eq:log_likelihood_gmm} \end{equation}$$
우리의 목적은 $L(\mathcal{X};\theta)$를 최대화하는 $\pi_k, \boldsymbol{\mu}_k, \Sigma_k$를 찾는 것이다. 주의할 점은 $\pi_k, \boldsymbol{\mu}_k, \Sigma_k$가 GMM에 하나씩 있는 것이 아니라, $K$개의 가우시안 분포마다 있는 것이기 때문에 GMM의 전체 매개변수는 총 $3K$개이다. 직관적으로 가능도 $L(\mathcal{X};\theta)$는 데이터의 분포를 정의하는 어떠한 매개변수 $\theta$가 주어졌을 때 우리가 관측한 데이터의 집합 $\mathcal{X}$가 나타날 확률이며, $L(\mathcal{X};\theta)$를 최대화하는 매개변수를 찾는다는 것은 주어진 데이터가 나타내는 분포를 가장 잘 근사하는 모델 매개변수를 찾는 것이다.
MLE를 기반으로 GMM의 매개변수를 직접 최적화하기 위해 아래의 식 $\eqref{eq:mle_mu}$와 같이 $L(\mathcal{X};\theta)$를 $\boldsymbol{\mu}_k$에 대해 미분한다.
$$\begin{equation}\begin{aligned}[b] \frac{\partial L(\mathcal{X};\theta)}{\partial \boldsymbol{\mu}_k} &= \sum_{n=1}^N \frac{\partial}{\partial \boldsymbol{\mu}_k} \left\{\log \left( \sum_{j=1}^K \pi_j \mathcal{N}(\textbf{x}_n; \boldsymbol{\mu}_j, \Sigma_j) \right) \right\} = 0\\\notag &\Leftrightarrow \sum_{n=1}^N \frac{\pi_k \mathcal{N}(\textbf{x}_n; \boldsymbol{\mu}_k, \Sigma_k)}{\sum_{j=1}^K \pi_j \mathcal{N}(\textbf{x}_n; \boldsymbol{\mu}_j, \Sigma_j)} \Sigma_k^{-1} (\textbf{x}_n - \boldsymbol{\mu}_k) = 0 \end{aligned} \label{eq:mle_mu} \end{equation}$$
그러나 $p(\textbf{x})$가 하나의 가우시안 분포로 정의된 경우와는 다르게 식 $\eqref{eq:mle_mu}$에는 로그함수 내부에 가우시안 분포의 합이 존재하기 때문에 $\boldsymbol{\mu}_k$에 대한 closed-form solution으로 정리되지 않는다. 따라서 기존의 MLE 대신 다른 방식으로 GMM의 매개변수를 최적화하기 위한 방법이 필요하다.
수리적 최적화에서는 어떠한 목적함수를 직접 최대화하는 것이 어려울 때 간접적으로 목적함수의 하한 (lower bound)을 최대화함으로써 최대화 문제를 해결한다. 잠재변수 (Latent variable) $\textbf{z}$를 도입하면 식 $\eqref{eq:lb_log_likelihood}$과 같이 우리가 최대화하고자 하는 GMM의 로그-가능도에 대한 하한을 찾을 수 있다.
$$\begin{equation}\begin{aligned}[b] L(\mathcal{X};\theta) &= \sum_{n=1}^N \log p(\textbf{x}_n;\theta)\\ &= \sum_{n=1}^N \log \left( \sum_{k=1}^K p(\textbf{x}_n, z_n=k;\theta) \right)\\ &= \sum_{n=1}^N \log \left(\sum_{k=1}^K q(z_n=k| \textbf{x}_n) \frac{p(\textbf{x}_n, z_n=k;\theta)}{q(z_n=k|\textbf{x}_n)}\right)\\ &= \sum_{n=1}^N \log \left( E_{z_n| \textbf{x}_n \sim q} \left[\frac{p(\textbf{x}_n, z_n;\theta)}{q(z_n| \textbf{x}_n)} \right] \right)\\ &\geq \sum_{n=1}^N E_{z_n| \textbf{x}_n \sim q} \left[\log\left(\frac{p(\textbf{x}_n, z_n;\theta)}{q(z_n| \textbf{x}_n)} \right)\right] \end{aligned} \label{eq:lb_log_likelihood} \end{equation}$$
식 $\eqref{eq:lb_log_likelihood}$에서 마지막 줄의 부등식은 Jensen's Inequality에 의해 유도되었다. 로그함수의 성질을 이용하면 $L(\mathcal{X};\theta)$의 하한을 최대화하는 매개변수 $\theta^*$는 아래와 같음을 알 수 있다.
$$\begin{equation}\begin{aligned}[b] \theta^* &= \underset{\theta}{\text{argmax}} \sum_{n=1}^N E_{z_n| \textbf{x}_n \sim q}\left[ \log p(\textbf{x}_n, z_n;\theta) \right]\\ &= \underset{\theta}{\text{argmax}} \sum_{n=1}^N E_{z_n| \textbf{x}_n \sim q}\left[ \log p(z_n;\theta) + \log p(\textbf{x}_n|z_n;\theta)\right] \end{aligned} \label{eq:argmax_theta} \end{equation}$$
식 $\eqref{eq:argmax_theta}$에서 $q(z_n| \textbf{x}_n)$은 매개변수 $\theta$에 대해 독립이기 때문에 최적화 과정에서 고려되지 않았다. 반면에 우리가 새로 도입한 잠재변수 $z_n$의 관점에서 보면 $L(\mathcal{X};\theta)$의 하한을 최대화하는 잠재변수의 확률분포 $q(z_n| \textbf{x}_n)$은 아래의 식 $\eqref{eq:argmax_z}$과 같이 유도된다.
$$\begin{equation}\begin{aligned}[b] q^* &= \underset{q}{\text{argmax}} \sum_{n=1}^N E_{z_n| \textbf{x}_n \sim q} \left[ \log p(\textbf{x}_n;\theta) + \log p(z_n|\textbf{x}_n;\theta) - \log q(z_n|\textbf{x}_n) \right]\\ &= \underset{q}{\text{argmax}} \; \sum_{n=1}^N \log p(\textbf{x}_n;\theta) - E_{z_n|\textbf{x}_n \sim q} \left[ \log \left(\frac{q(z_n|\textbf{x}_n)}{p(z_n|\textbf{x}_n;\theta)} \right) \right]\\ &= \underset{q}{\text{argmin}} \; \sum_{n=1}^N D_{KL}(q(z_n|\textbf{x}_n)||p(z_n|\textbf{x}_n;\theta)) \end{aligned} \label{eq:argmax_z} \end{equation}$$
데이터의 분포 $p(\textbf{x}_n;\theta)$는 $z_n$에 대해 독립이므로 잠재변수에 대한 최적화 과정에서 고려되지 않는다. 식 $\eqref{eq:argmax_z}$에서 $D_{KL}$은 두 확률분포의 차이를 의미하는 Kullback–Leibler divergence이다.
일반적으로 GMM을 비롯한 혼합모델 (mixture model)에서는 잠재변수 $z_n$을 $n$번째 데이터 $\textbf{x}_n$이 몇 번째 mixture component (GMM에서는 가우시안 분포)에서 생성되었는지를 나타내는 확률변수로 정의한다. 이러한 정의에 따라 $z_n$은 이산확률변수가 되며, $\{1, 2, ..., K\}$ 중 하나의 값을 갖는다.
잠재변수 $z_n$을 도입하면 $L(\mathcal{X};\theta)$의 하한을 최대화하는 매개변수 $\theta^*$는 아래와 같이 계산된다.
$$\begin{equation}\begin{aligned}[b] \theta^* &= \underset{\theta}{\text{argmax}} \sum_{n=1}^N E_{z_n|\textbf{x}_n \sim q} \left[\log p(z_n;\theta) + \log p(\textbf{x}_n|z_n;\theta) \right]\\ &= \underset{\theta}{\text{argmax}} \sum_{n=1}^N \sum_{k=1}^K q(z_n=k|\textbf{x}_n) (\log \pi_k + \log \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_k, \Sigma_k)) \end{aligned} \label{eq:argmax_theta_latent} \end{equation}$$
식 $\eqref{eq:log_likelihood_gmm}$의 목적함수 $L(\mathcal{X};\theta)$와 식 $\eqref{eq:argmax_theta_latent}$의 목적함수를 비교하면 잠재변수를 도입한 모델의 이점이 명확해진다. 식 $\eqref{eq:log_likelihood_gmm}$에서는 로그함수 내부에 $K$개의 확률밀도함수에 대한 합성연산이 있어서 미분이 어려웠다면, 식 $\eqref{eq:argmax_theta_latent}$에서는 로그함수 내부에 확률밀도함수에 대한 합성연산이 없어졌다. 다음 항목에서는 식 (6-9)의 과정을 통해 유도한 내용을 바탕으로 GMM의 매개변수를 최적화하기 위한 학습 알고리즘에 대해 설명한다.
일반적으로 GMM의 모델 매개변수는 기댓값 최대화 알고리즘 (expectation-maximization algorithm, EM 알고리즘)을 이용하여 최적화한다. EM 알고리즘은 가능도 대신 가능도의 기댓값을 최대화하여 모델 매개변수를 최적화하며, 이러한 접근법이 수학적으로 유효한 이유는 식 $\eqref{eq:lb_log_likelihood}$에서 설명했다.
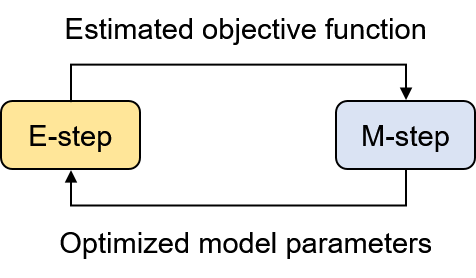
EM 알고리즘은 그림 2와 같이 expectation step (E-step)과 maximization step (M-step)이라는 두 단계를 반복하여 가능도의 기댓값을 최대화하는 매개변수를 찾는다. EM 알고리즘의 각 단계는 아래와 같은 작업을 수행한다.
- Expectation step (E-step): 가능도의 기댓값을 계산하기 위해 필요한 인자들을 추정한다. 식 $\eqref{eq:argmax_theta_latent}$를 예로 들면 모델 매개변수는 아니지만 가능도 계산에 필요한 $\gamma_k(\textbf{x}_n) = q(z_n=k|\textbf{x}_n)$을 추정한다.
- Maximization step (M-step): 추정된 가능도의 기댓값에 대해 이를 최대화하는 매개변수를 찾는다. GMM에서는 M-step에서 모델 매개변수에 해당하는 $\pi_k, \boldsymbol{\mu}_k, \Sigma_k$를 최적화한다.
요약하자면 GMM의 학습은 식 $\eqref{eq:argmax_theta_latent}$에서 정의한 식 $\eqref{eq:obj_func_gmm}$의 목적함수 $J(\mathcal{X};\theta)$를 최대화하는 매개변수를 EM 알고리즘을 이용하여 찾는 것이다.
$$\begin{equation} J(\mathcal{X};\theta) = \sum_{n=1}^N \sum_{k=1}^K \gamma_k(\textbf{x}_n) (\log \pi_k + \log \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_k, \Sigma_k)) \label{eq:obj_func_gmm} \end{equation}$$
아래에서는 GMM의 모델 매개변수 학습을 위한 EM 알고리즘의 E-step과 M-step을 수학적으로 유도한다.
4.1. Expectation Step (E-Step)
먼저 E-step에 해당하는 $\gamma_k(\textbf{x}_n) = q(z_n=k|\textbf{x}_n)$의 추정은 아래의 식 $\eqref{eq:e_step}$과 같이 수행된다.
$$\begin{equation}\begin{aligned}[b] q(z_n=k|\textbf{x}_n) &= \frac{p(z_n=k)p(\textbf{x}_n|z_n=k)}{p(\textbf{x}_n)}\\ &= \frac{\pi_k \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_k, \Sigma_k)}{\sum_{j=1}^K \pi_j \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_j, \Sigma_j)} \end{aligned} \label{eq:e_step} \end{equation}$$
식 $\eqref{eq:e_step}$은 현재의 모델 매개변수를 이용하여 $J(\mathcal{X};\theta)$의 계산에 필요한 $\gamma_k(\textbf{x}_n)$을 계산할 수 있음을 보여준다.
4.2. Maximization Step (M-Step)
M-step에서는 추정된 $\gamma_k(\textbf{x}_n)$을 기반으로 GMM의 모델 매개변수 $\pi_k, \boldsymbol{\mu}_k, \Sigma_k$를 최적화한다. 먼저 $\boldsymbol{\mu}_k$를 최적화하기 위해 $J(\mathcal{X};\theta)$를 $\boldsymbol{\mu}_k$에 대해 미분하면 아래와 같다.
$$\begin{equation}\begin{aligned}[b] \frac{\partial J(\mathcal{X};\theta)}{\partial \boldsymbol{\mu}_k} &= \sum_{n=1}^N \gamma_k(\textbf{x}_n) (\textbf{x}_n - \boldsymbol{\mu}_k) = 0\\ &\Leftrightarrow \boldsymbol{\mu}_k = \frac{\sum_{n=1}^N \gamma_k(\textbf{x}_n) \textbf{x}_n}{\sum_{n=1}^N \gamma_k(\textbf{x}_n)} \end{aligned} \label{eq:m_step_mu} \end{equation}$$
그 다음, $J(\mathcal{X};\theta)$를 $\Sigma_k$에 대해 미분하면 아래와 같다.
$$\begin{equation} \begin{aligned}[b] \frac{\partial J(\mathcal{X};\theta)}{\partial \Sigma_k} &= \sum_{n=1}^N \gamma_k(\textbf{x}_n) \left[-\frac{1}{2}\frac{\partial}{\partial \Sigma_k}\left\{\log |\text{det}(\Sigma_k)| + (\textbf{x}_n - \boldsymbol{\mu}_k)^T \Sigma_k^{-1} (\textbf{x}_n - \boldsymbol{\mu}_k) \right\} \right] = 0\\ &\Leftrightarrow \sum_{n=1}^N \gamma_k(\textbf{x}_n) \left\{\Sigma_k^{-1} - \Sigma_k^{-1} (\textbf{x}_n - \boldsymbol{\mu}_k)(\textbf{x}_n - \boldsymbol{\mu}_k)^T \Sigma_k^{-1} \right\} = 0\\ &\Leftrightarrow \sum_{n=1}^N \gamma_k(\textbf{x}_n) \Sigma_k = \sum_{n=1}^N \gamma_k(\textbf{x}_n) (\textbf{x}_n - \boldsymbol{\mu}_k)(\textbf{x}_n - \boldsymbol{\mu}_k)^T\\ &\Leftrightarrow \Sigma_k = \frac{\sum_{n=1}^N \gamma_k(\textbf{x}_n) (\textbf{x}_n - \boldsymbol{\mu}_k)(\textbf{x}_n - \boldsymbol{\mu}_k)^T}{\sum_{n=1}^N \gamma_k(\textbf{x}_n)} \end{aligned} \label{eq:m_step_sigma} \end{equation}$$
식 $\eqref{eq:m_step_sigma}$의 유도 과정에서는 공분산 행렬 $\Sigma_k$가 갖는 positive semidefinite 및 symmetric 성질이 활용되었다. 공분산 행렬은 positive semidefinite 행렬이기 때문에 음수가 아닌 행렬식 $\text{det}(\Sigma_k)$를 가지며, 또한 symmetric 행렬이기 때문에 $\Sigma_k^T = \Sigma_k$이다. $\Sigma_k$에 관한 미분 과정은 Matrix Cookbook을 참고하면 쉽게 이해할 수 있다.
마지막으로 $\pi_k$를 최적화하기 위해 $\pi_k$에 대해 $J(\mathcal{X};\theta)$를 미분한다. 그러나 $\pi_k$는 식 $\eqref{eq:const_pi}$의 제약조건을 만족해야하기 때문에 식 $\eqref{eq:obj_pi_lag}$와 같이 라그랑주 승수법 (Lagrange multiplier method)을 적용한 목적함수 $J_{\lambda}(\mathcal{X};\theta)$에 대해 미분을 수행한다.
$$\begin{equation} J_{\lambda}(\mathcal{X};\theta) = \sum_{n=1}^N \sum_{k=1}^K \gamma_k(\textbf{x}_n) (\log \pi_k + \log \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_k, \Sigma_k)) + \lambda \left(1 - \sum_{k=1}^K \pi_k \right) \label{eq:obj_pi_lag} \end{equation}$$
식 $\eqref{eq:obj_pi_lag}$의 Lagrange multiplier $\lambda$는 제약조건에 관한 새로운 변수이며, $J_{\lambda}(\mathcal{X};\theta)$를 $\pi_k$에 대해 미분하면 아래와 같다.
$$\begin{equation}\begin{aligned}[b] \frac{\partial J_{\lambda}(\mathcal{X};\theta)}{\partial \pi_k} &= \sum_{n=1}^N \frac{\gamma_k(\textbf{x}_n)}{\pi_k} - \lambda = 0\\ &\Leftrightarrow \pi_k = \frac{1}{\lambda} \sum_{n=1}^N \gamma_k(\textbf{x}_n) \end{aligned} \label{eq:m_step_pi} \end{equation}$$
$\sum_{k=1}^K \pi_k = 1$및 $\sum_{k=1}^K \gamma_k(\textbf{x}_n) = 1$이라는 두 성질을 이용하면 식 $\eqref{eq:m_step_pi}$를 아래와 같이 변환할 수 있다.
$$\begin{equation} \sum_{k=1}^K \pi_k = \frac{1}{\lambda} \sum_{n=1}^N \sum_{k=1}^K \gamma_k(\textbf{x}_n) \label{eq:m_step_pi_imd} \end{equation}$$
식 $\eqref{eq:m_step_pi_imd}$을 통해 Lagrange multiplier $\lambda$는 아래와 같이 상수로 계산된다.
$$\begin{equation} \lambda = N \label{eq:lambda} \end{equation}$$
이것을 식 $\eqref{eq:m_step_pi}$에 대입하면 $\pi_k$는 식 $\eqref{eq:opt_pi}$과 같이 계산된다.
$$\begin{equation} \pi_k = \frac{1}{N} \sum_{n=1}^N \gamma_k(\textbf{x}_n) \label{eq:opt_pi} \end{equation}$$
따라서 M-step에서는 식 (12, 13, 18)을 이용하여 GMM의 모델 매개변수인 $\boldsymbol{\mu}_k$, $\Sigma_k$, $\pi_k$를 최적화한다. 그리고 최적화된 모델 매개변수를 이용하여 다시 E-step으로 돌아가서 $\gamma_k(\textbf{x})$를 계산하고 M-step을 반복한다.
분류 문제에서 GMM을 구성하는 $K$개의 가우시안 분포는 각각이 하나의 데이터 범주 (class)를 의미하며, 입력 데이터 $\textbf{x}$에 대한 분류 문제는 $\gamma_k(\textbf{x}) = q(z = k|\textbf{x})$가 최대가 되는 $k$를 찾는 것과 같다. GMM의 학습이 완료되었다면 우리는 이미 최적화된 모델 매개변수 $\boldsymbol{\mu}_k^*, \Sigma_k^*, \pi_k^*$를 갖고있기 때문에 식 $\eqref{eq:e_step}$을 이용하여 학습 데이터셋에 최적화된 $\gamma_k(\textbf{x})$을 계산할 수 있다. 따라서 입력 데이터 $\textbf{x}$에 대해 $y$를 GMM이 예측한 class label이라고 하면, GMM을 이용한 데이터 분류 과정은 아래의 식 $\eqref{eq:classification}$와 같이 정의된다.
$$\begin{equation} y = \underset{1, 2, ..., K}{\text{argmax}} \frac{\pi_k \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_k, \Sigma_k)}{\sum_{j=1}^K \pi_j \mathcal{N}(\textbf{x}_n;\boldsymbol{\mu}_j, \Sigma_j)} \label{eq:classification} \end{equation}$$
'머신러닝 > 확률모델' 카테고리의 다른 글
| Unbiased and Biased Estimators의 개념과 머신러닝 (1) | 2024.01.11 |
|---|---|
| 몬테카를로 방법 (Monte Carlo Method)과 베이지안 머신러닝 (4) | 2024.01.07 |
| Reparameterization Trick에 대한 수학적 이해와 기댓값의 미분가능성 (2) | 2023.12.21 |
| Conjugate Prior의 정의와 예제 (0) | 2023.12.18 |
| 선형회귀 (Linear Regression)에 대한 여러 접근법 (0) | 2023.12.09 |