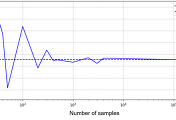
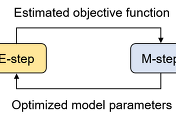
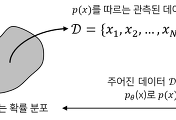
확률모델의 학습에서 우리의 목적은 주어진 샘플 (데이터) $\textbf{x}_1, \textbf{x}_2, ..., \textbf{x}_n$으로부터 데이터를 생성한 확률분포 $p(\textbf{x}|\theta)$의 참된 매개변수 $\theta$를 찾는 것이다. 그러나 대부분의 머신러닝 응용에서는 모든 데이터를 관측할 수 없기 때문에 추정된 매개변수 $\tilde{\theta}$는 참된 매개변수 $\theta$와 차이가 있을 것이다. 통계학에서 편향 (bias)은 추정된 매개변수와 참된 매개변수의 차이를 말하며, 편향은 추정된 매개변수의 기댓값을 기반으로 식 $\eqref{eq:bias}$과 같이 정의된다.
$$\begin{equation} \text{Bias}(\tilde{\theta}, \theta) = E_{p(\textbf{x}|\theta)}[\tilde{\theta}] - \theta\label{eq:bias}\end{equation}$$
Unbiased estimator와 biased estimator는 식 $\eqref{eq:bias}$을 기반으로 아래와 같이 정의된다.
- Unbiased estimator: 추정한 $\tilde{\theta}$에 대해 $E_{p(\textbf{x}|\theta)}[\tilde{\theta}] - \theta = 0$인 모델
- Biased estimator: 추정한 $\tilde{\theta}$에 대해 $E_{p(\textbf{x}|\theta)}[\tilde{\theta}] - \theta \neq 0$인 모델
Unbiased estimator와 biased estimator에 대한 예시는 아래와 같다.
평균이 $\mu$인 확률분포에서 추출된 $n$개의 서로 독립인 샘플 $X_1, X_2, ..., X_n$에 대해 표본평균 $\tilde{\mu}$의 기댓값은 아래의 식 $\eqref{eq:sample_mean}$와 같다.
$$\begin{equation}\begin{aligned}[b] E[\tilde{\mu}] &= E\left[\frac{1}{n}\sum_{i=1}^n X_i \right]\\ &= \frac{1}{n} \sum_{i=1}^n E[X_i]\\ &= \frac{1}{n}\sum_{i=1}^n \mu\\ &= \mu \end{aligned}\label{eq:sample_mean}\end{equation}$$
따라서 $E[\tilde{\mu}] - \mu = 0$이므로, 표본평균으로 확률분포의 평균 $\mu$를 계산하는 모델은 unbiased estimator이다.
분산이 $S$인 확률분포에서 추출된 $n$개의 서로 독립인 샘플 $X_1, X_2, ..., X_n$에 대해 표본분산 $\tilde{S}$의 기댓값은 아래의 식 $\eqref{eq:sample_var}$과 같다.
$$\begin{equation}\begin{aligned}[b] E[\tilde{S}] &= E \left[\frac{1}{n}\sum_{i=1}^n (X_i - \tilde{\mu})^2 \right]\\ &= \frac{1}{n} E \left[\sum_{i=1}^n X_i^2 - 2\tilde{\mu} \sum_{i=1}^n X_i + \sum_{i=1}^n \tilde{\mu}^2 \right]\\ &= \frac{1}{n} \left(\sum_{i=1}^n E\left[X_i^2 \right] - n E[\tilde{\mu}^2] \right)\\ &= \frac{1}{n} \left( nS + n\mu^2 - S - n\mu^2 \right)\\ &= \frac{n-1}{n}S \end{aligned}\label{eq:sample_var}\end{equation}$$
따라서 $E[\tilde{S}] - S \neq 0$이므로, 표본분산으로 확률분포의 분산 $S$를 계산하는 모델은 biased estimator이다.
분산을 추정하기 위한 unbiased estimator는 식 $\eqref{eq:sample_var}$에서 $n$으로 나누는 것이 아니라, $n-1$로 나누는 것이다. 만약 $n-1$로 나눈다면 표본분산은 아래와 같이 실제 분산 $S$와 같아진다.
$$\begin{equation}\begin{aligned}[b] E[\tilde{S}] &= E \left[\frac{1}{n-1}\sum_{i=1}^n (X_i - \tilde{\mu})^2 \right]\\ &= \frac{1}{n-1} E \left[\sum_{i=1}^n X_i^2 - 2\tilde{\mu} \sum_{i=1}^n X_i + \sum_{i=1}^n \tilde{\mu}^2 \right]\\ &= \frac{1}{n-1} \left(\sum_{i=1}^n E\left[X_i^2 \right] - n E[\tilde{\mu}^2] \right)\\ &= \frac{1}{n-1} \left( nS + n\mu^2 - S - n\mu^2 \right)\\ &= S \end{aligned}\label{eq:sample_ub_var}\end{equation}$$
따라서 $n-1$로 나눈 estimator에서는 식 $\eqref{eq:sample_ub_var}$와 같이 $E[\tilde{S}] - S = 0$이므로, 이 모델은 확률분포의 분산을 추정하기 위한 unbiased estimator이다.

머신러닝에서는 일반적으로 실제 확률분포의 매개변수와 차이가 있는 biased estimator보다는 차이가 없는 unbiased estimator를 선호한다. 그러나 항상 unbiased estimator가 biased estimator보다 좋다고는 말할 수 없는데, 이는 아래의 식 $\eqref{eq:bias_var_tradeoff}$로 정의되는 편향-분산 트레이드오프 (bias-variance tradeoff)에 의해 설명된다.
$$\begin{equation} \text{E}[(y - f(\textbf{x}))^2] = \sigma^2 + (\underbrace{\text{E}[f^*(\textbf{x}) - f(\textbf{x})]}_{= \; \text{bias of} \; f})^2 + \underbrace{\text{Var}[f(\textbf{x})]}_{= \; \text{variance of} \; f} \label{eq:bias_var_tradeoff} \end{equation}$$
어떠한 머신러닝 모델 $f: \mathcal{X} \rightarrow \mathcal{Y}$의 손실함수는 식 $\eqref{eq:bias_var_tradeoff}$와 같이 편향 (bias)과 분산 (variacne)로 분해된다. 모델 $f$의 손실함수를 최소화하기위해서는 편향과 분산을 동시에 최소화해야 한다. 편향이 0이 되는 모델 $f^*$가 바로 unbiased estimator이지만, 편향이 0이 될만큼 모델이 복잡해지면 모델 복잡도에 의해 분산이 증가할 수 있다. 이러한 편향-분산 트레이드오프에 관한 자세한 내용은 이 문서에 서술되어있다.
'머신러닝 > 확률모델' 카테고리의 다른 글
| 편향-분산 트레이드오프 (Bias-Variance Tradeoff)와 L2 규제 (L2 Regularization) (5) | 2024.01.15 |
|---|---|
| 몬테카를로 방법 (Monte Carlo Method)과 베이지안 머신러닝 (3) | 2024.01.07 |
| [머신러닝] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)과 EM 알고리즘 (21) | 2023.12.29 |
| Reparameterization Trick에 대한 수학적 이해와 기댓값의 미분가능성 (2) | 2023.12.21 |
| Conjugate Prior의 정의와 예제 (0) | 2023.12.18 |