[파일구조] - 트리 구조를 이용한 인덱스 관리

1. 트리 구조를 이용한 인덱스 관리

이전의 배열이나 inverted list를 이용한 인덱스 체계의 문제점을 극복하고자 인덱스를 트리 구조로 관리하는 것에 대한 많은 연구가 이루어졌다. 인덱스를 관리하기 위한 자료 구조를 고안할 때는 반드시 아래와 같은 사항을 고려해야 한다.

• 인덱스를 정렬된 상태로 유지할 수 있어야 하며, 인덱스를 정렬하는 비용을 최소화해야 한다.
• 인덱스의 추가(insertion), 삭제(deletion)을 효율적으로 수행할 수 있어야 한다.
• 인덱스를 효율적으로 검색할 수 있어야 한다.

이러한 세 가지 요구 사항을 만족시킬 수 있는 자료 구조로는 이진 탐색 트리가 있다. 이진 탐색 트리는 아래의 그림과 같이 모든 데이터를 정렬된 상태로 보관하며, 각 노드는 2개 이하의 자식 노드만 가질 수 있다.

그러나 이진 탐색 트리의 검색은 이진 탐색을 기반으로 수행된다. 메모리 상에서 이진 탐색은 매우 효율적인 탐색 알고리즘이다. 그러나 하드디스크 상에서 이진 탐색은 수 많은 임의 접근(random access)를 발생시키기 때문에 오히려 순차 탐색(sequential search)보다 비효율적일 수도 있다. 또한, 아래의 그림과 같이 이진 탐색 트리가 비대칭적으로 형성되면 이진 탐색 트리의 탐색 효율은 급격히 감소한다.

2. AVL 트리

이진 탐색 트리에서 비대칭적 구조에 의한 탐색 효율의 저하를 방지하기 위해서는 트리가 비대칭적으로 형성되는 것을 방지해야 한다. 즉, 주어진 데이터로부터 균형 잡힌(balanced) 구조의 트리를 생성하도록 연산을 구현해야 한다. 자료 구조에서는 다음의 정의에 부합하는 트리 구조를 height-balanced tree라고 한다.

트리를 구성하는 어떠한 노드의 좌측과 우측 subtree의 높이 차이가 1 이하인 트리

Height-balanced tree의 정의를 수학적으로 나타내면 다음과 같이 나타낼 수 있다.

• Empty tree는 height-balanced tree이다.

• 어떠한 non-empty binary tree T의 왼쪽 subtree를 ${T}_{L}$, 오른쪽 subtree를 ${T}_{R}$이라고 할 때, ${T}_{L}$과 ${T}_{R}$이 모두 height-balanced tree이고 아래의 식을 만족하면 T는 height-balanced tree이다.

아래의 그림은 height-balanced tree의 몇 가지 예시를 나타낸다.

위의 정의와 같은 height-balanced tree를 AVL 트리라고 한다. AVL 트리의 이러한 속성 때문에 AVL 트리를 HB(1) tree라고 부르기도 한다.

AVL 트리를 이용함으로써 트리가 비대칭적으로 생성되는 것을 방지할 수 있기 때문에 탐색의 효율은 ${log}_{2}$$n$에 근접한다. 그러나 AVL 트리를 파일 시스템이 적용하기에는 아직 아래와 같은 문제점이 존재한다.

• AVL 트리는 자식 노드를 2개까지 밖에 가질 수 없기 때문에 트리의 높이가 비효율적으로 커지는 문제가 있다.
• AVL 트리 또한 이진 탐색을 이용하기 때문에 많은 seek 연산을 발생시킨다.

3. Paged Binary Tree

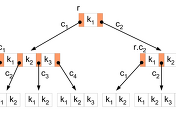
AVL 트리는 트리가 비대칭적으로 생성되는 문제점을 해결하였지만, 이진 탐색 자체가 갖고 있는 문제점은 해결할 수 없었다. Paged binary tree는 이진 탐색 자체가 갖고 있는 문제점을 해결하기 위해 고안된 트리 구조로써, 이진 트리를 페이지 단위로 분리하여 하드디스크상의 연속된 공간에 저장한다. 아래의 그림은 한 페이지에 7개의 노드를 저장하도록 구현된 paged binary tree의 한 예시를 보여준다.

Paged binary tree를 이용하여 이진 탐색을 수행할 때, 위와 같은 page binary tree에서는 단 두 번의 seek 연산만으로 원하는 데이터를 읽을 수 있다. 예를 들어, 위의 그림에서 붉은색으로 칠해진 노드의 데이터를 하드디스크에서 읽는다고 가정하면 다음의 과정을 통해 데이터를 읽을 수 있다.

1) 하드디스크에서 Page 1을 읽은 다음, Page 1로부터 생성된 이진 트리에서 이진 탐색을 수행한다 (1회의 seek 연산 발생).

2) 이진 탐색의 결과 붉은색으로 칠해진 노드의 데이터가 Page 3에 저장되어 있다는 결과를 얻게 되고, 하드디스크에서 Page 3를 읽는다 (1회의 seek 연산 발생). 

그러나 paged binary tree 또한 아래와 같은 문제점을 갖고 있다.

• Paged binary tree의 각 페이지는 reference field를 포함하고 있기 때문에 하드디스크의 공간이 낭비된다. 위의 paged binary tree에서는 각 페이지 당 14개의 reference field를 저장해야 한다.
• 데이터가 정렬되지 않은 임의의 순서로 입력될 때, paged binary tree를 올바르게 구성하는 것은 매우 복잡한 문제이다.
• 어떠한 경우에는 한 페이지에 노드가 1~2개 저장되는 것처럼 너무 적은 수의 노드만 저장될 수 있는데, 이러한 경우에는 심각한 내부 단편화가 발생하게 된다.

AVL 트리와 paged binary tree가 갖고 있는 문제점을 해결하기 위해 B 트리가 연구되었다.