Insert 연산은 인자로 전달받은 key를 B 트리에 추가하는 연산으로써, B 트리의 insert 연산은 다른 종류의 트리에 비해 매우 복잡하다. B 트리의 insert 연산은 아래와 같은 과정으로 수행된다.
1) 새로운 key 값이 입력될 leaf node를 탐색한다. B 트리에서 leaf node를 탐색하는 과정은 이진 탐색 트리(binary search tree)에서 주어진 값에 대한 노드를 찾는 과정과 유사하다.
2) 선택된 leaf node의 모든 key 값 중에서 새로운 key 값이 가장 크다면, 선택된 leaf node의 가장 큰 key 값에 대한 정보를 모두 새로운 key 값으로 변경한다. 이러한 변경은 B 트리 전체에서 발생한다.
3) 새로운 key 값을 선택된 leaf node에 추가한다.
4) 선택된 노드(선택된 leaf node)에서 overflow가 발생하였다면 5로 이동하고, 발생하지 않았다면 11로 이동한다.
5) 선택된 노드를 두 개로 분리하고, 선택된 노드의 상위 층으로 이동한다.
6) 만약, 선택된 노드의 상위 층이 root node가 존재하는 층이면 10으로 이동하고, 그렇지 않다면 7로 이동한다.
7) Parent node에 저장되어 있는 선택된 노드의 가장 큰 key 값에 대한 정보를 변경한다.
8) 선택된 노드의 분리로 인해 새롭게 생성된 노드의 가장 큰 key 값을 parent node에 추가한다.
9) Parent node에서 overflow가 발생하였다면, 현재 선택된 노드를 parent node로 변경하고 5부터 다시 연산을 실행한다.
10) Root node 이전 층까지 overflow가 발생하였다면, 새로운 Root node를 생성하고, 선택된 노드로부터 분리된 두 노드에 대한 정보를 root node에 저장한다.
11) 연산을 종료한다.
Search 연산은 B 트리를 탐색하여 주어진 key 값에 해당하는 데이터를 반환하는 연산으로써, insert 연산에 비하면 매우 간단하다.
1) 새로운 key 값이 입력될 leaf node를 탐색한다. B 트리에서 leaf node를 탐색하는 과정은 이진 탐색 트리(binary search tree)에서 주어진 값에 대한 노드를 찾는 과정과 유사하다.
2) 찾은 leaf node에서 주어진 key 값과 일치하는 데이터를 반환한다.
Merge 연산은 두 개의 노드를 하나의 노드로 병합하는 연산이다. B 트리에서 merge 연산은 leaf node의 key를 제거하는 remove 연산의 실행 결과, underflow가 발생한 노드가 존재하면 실행된다. B 트리에서 underflow라는 것은 어떠한 노드에 B 트리에서 허용하는 최소 데이터의 수보다 적은 수의 데이터가 저장되어 있는 경우를 의미한다. B 트리의 merge 연산은 아래와 같은 과정으로 수행된다.
1) Underflow가 발생한 노드가 존재하는지 검사한다. B 트리에서 underflow는 어떤 노드가 $[order / 2]$보다 적은 수의 key를 저장하고 있는 경우를 의미한다.
2-1) Underflow가 발생한 노드의 이웃 노드에 key를 저장할 수 있는 공간이 있다면, underflow가 발생한 노드의 key를 이웃 노드로 이동시킨다. 즉, underflow가 발생한 노드와 이웃 노드를 병합한다.
2-2) Underflow가 발생한 노드의 어떠한 이웃 노드에도 key를 저장할 충분한 공간이 존재하지 않는다면, merge 연산이 실패했음을 반환한다.
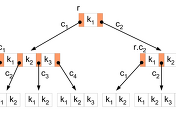
Merge 연산은 B 트리의 다른 연산에 비하면 비교적 간단하다. 그러나 merge 연산의 가장 큰 문제점은 언제나 연산이 성공한다는 것을 보장하지 않는다는 것이다. 예를 들어, 아래의 그림에서 Y를 제거한다고 가정하면, 이웃 노드에 이미 5개의 key가 저장되어 있기 때문에 merge 연산이 불가능하다.
Merge 연산의 단점은 key를 하나의 leaf node에 밀집시킨다는 것이다. 예를 들어, 위의 그림에서 B가 제거되어 A와 D가 이웃 노드에 병합된다고 가정하면 ABD의 이웃 노드인 FHJ는 key를 저장을 위해 할당된 5개의 공간을 모두 사용하게 된다.
이렇게 key를 하나의 leaf node에 밀집시키면, insert 연산 시 leaf node를 분리해야하는 경우가 더 빈번하게 발생한다. Insert 연산에 나타나듯이 leaf node를 분리하는 작업은 parent node에 대해서도 분리 연산을 반복적으로 수행해야 하기 때문에 많은 비용이 든다.
B 트리의 redistribute 연산은 remove 연산으로 인해 underflow가 발생한 노드를 이웃 노드에 병합하는 것이 아니라, 충분한 수의 key를 저장하고 있는 이웃 노드의 key를 underflow가 발생한 노드로 이동시키는 것이다. Redistribute 연산의 과정은 아래의 그림과 같다.
Redistribute 연산을 이용하면, merge 연산을 이용할 때보다 leaf node의 데이터 밀집도가 감소하여 insert 연산 시, leaf node를 분리하는 경우가 더 적게 발생하는 이점이 있다. 그러나 위의 그림에서 ABD 노드의 B가 제거되는 경우에는 redistribute 연산을 이용할 수가 없다. 따라서, B 트리를 구현할 때는 상황에 맞게 merge 연산과 redistribute 연산을 호출하도록 구현해야 한다.
Remove 연산은 주어진 key 값에 해당하는 데이터를 B 트리에서 제거하는 연산으로써, B 트리의 remove 연산은 경우에 따라 두 노드를 병합(merge)하거나 재배치(redistribution)해야하기 때문에 연산의 과정이 매우 복잡하다. Remove 연산을 수행할 때는 아래와 같은 네 가지 경우가 발생한다. $N$은 remove 연산의 대상이 되는 노드이며, $k$는 제거하려는 key 값이다.
- $k$가 $N$에서 가장 큰 값을 갖는 key가 아니고, $k$를 제거하여도 $N$에는 최소 key의 수보다 많은 key가 저장되어 있을 때는 단순히 $k$를 제거하기만 하면 된다.
- $k$가 $N$에서 가장 큰 값을 갖는 key 이고, $k$를 제거하여도 $N$에는 최소 key의 수보다 많은 key가 저장되어 있을 때는 $k$를 제거하고 상위 노드에 저장된 가장 큰 key 값에 대한 정보를 변경한다.
- $k$를 제거하여 $N$에 underflow가 발생하였고, $N$의 이웃 노드에는 $N$의 남은 데이터를 저장할 충분한 공간이 있을 때, $N$을 이웃 노드에 대해 merge 연산을 실행한다.
- $k$를 제거하여 $N$에 underflow가 발생하였고, $N$의 이웃 노드들에는 $N$의 남은 데이터를 저장할 충분한 공간이 없을 때, $N$과이웃 노드에 대해 redistribute 연산을 실행한다. 그 다음, 상위 노드에 저장된 가장 큰 key 값에 대한 정보를 변경한다.
'객체지향설계' 카테고리의 다른 글
| [파일구조] - Indexed Sequential File (1) | 2016.06.12 |
|---|---|
| [파일구조] - Virtual B 트리 (0) | 2016.06.12 |
| [파일구조] - B 트리 (0) | 2016.06.11 |
| [파일구조] - 트리 구조를 이용한 인덱스 관리 (0) | 2016.06.11 |
| [파일구조] - 인덱스 파일의 구현 II (0) | 2016.06.10 |