[확산 모델] - 확산 모델 (Diffusion Model)의 정의와 Denoising Diffusion Probabilistic Model (DDPM)

1. Diffusion Model (확산 모델)의 개념과 DDPM

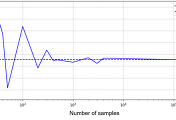
자연계에서는 그림 1과 같이 초기에는 특정 분포에 따라 존재하던 입자가 최종적으로 균일하게 분포하는 확산 (diffusion) 현상이 발생한다. Diffusion model은 이러한 자연계의 확산 과정을 기반으로 고안된 생성형 머신러닝 방법론이다 [1].

그림 1. 확산 과정 (https://en.wikipedia.org/wiki/Diffusion).

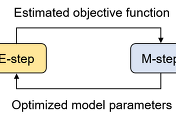
Diffusion model은 기본적으로 그림 2와 같이 forward process와 reverse process로 구성된다. Forward process는 원본 데이터 $x_0$를 최종 노이즈 $x_T$로 변환하는 과정이고, reverse process는 최종 노이즈 를 원본 데이터 $x_0$로 변환하는 과정이다. Diffusion model은 reverse process를 학습함으로써 임의의 노이즈 $x_T$로부터 데이터 $x_0$를 만들어내는 생성형 모델로 사용될 수 있다.

그림 2. Diffusion model의 개념 및 구조.

Denoising diffusion probabilistic model (DDPM) [2]은 forward process와 reverse process를 확률 과정으로 정의하였으며, diffusion model의 동작을 이해하는데 기초가 되는 방법론이다. 이 글에서는 DDPM의 구조와 DDPM을 유도하기 위한 수학적 과정에 대해 소개한다.

 

2. Forward Process

Forward process의 목적은 원본 데이터 $x_0$를 최종 noise $x_T$로 변환하는 것이다. Forward process는 새로운 데이터를 생성하는 reverse process를 학습할 때 이용된다. Forward process는 Markov chain을 기반으로 아래의 식 $\text{(1)}$과 같이 정의된다.

$$\begin{array}{}\text{(1)}& q(x_T,x_{T-1},...,x_1|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1}).\end{array}$$

일반적으로 foward process를 구성하는 각 확률분포 $q(x_t|x_{t-1})$는 식 $\text{(2)}$와 같이 정규 분포 (normal distribution)를 기반으로 정의된다.

$$\begin{array}{}\text{(2)}& q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathbf{\text{I}}).\end{array}$$

${\beta }_1,...,{\beta }_T\in (0,1)$는 원본 데이터 $x_0$에 Gaussian noise를 더해가는 속도를 조절하는 hyperparameter이다. 식 $\text{(2)}$과 같이 forward process를 정의하면, 원본 데이터 $x_0$가 주어졌을 때 $q(x_t|x_0)$에서 $x_t$를 바로 샘플링할 수 있다는 장점이 있는데, 자세한 내용은 아래에서 설명한다.

 

3. Reverse Process

Reverse process의 목적은 최종 noise $x_T$에서 원본 데이터 $x_0$를 복원하는 것이다. Diffusion model의 핵심은 주어진 데이터셋으로부터 reverse process를 학습하고, 이를 바탕으로 noise로부터 새로운 데이터를 생성하는 것이다. Reverse process도 Markov chain을 기반으로 식 $\text{(3)}$와 같이 정의된다.

$$\begin{array}{}\text{(3)}& p(x_0,x_1,...,x_T)=p(x_T)\prod _{t=1}^{T}p(x_{t-1}|x_t).\end{array}$$

위의 Reverse process에 대해 process의 시작점인 noise $x_T$의 확률분포 $p(x_T)$는 식 $\text{(4)}$와 같이 가정한다.

$$\begin{array}{}\text{(4)}& p(x_T)=\mathcal{N}(x_T;\mathbf{\text{0}},\mathbf{\text{I}}).\end{array}$$

그 다음, 각 확률분포를 식 $\text{(5)}$과 같이 매개변수화된 정규분포로 정의한다.

$$\begin{array}{}\text{(5)}& p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mathit{\mu }}_{\theta }(x_t,t),{\mathbf{\Sigma }}_{\theta }(x_t,t)).\end{array}$$

위의 식에서 ${\mathit{\mu }}_{\theta }(x_t,t)$와 ${\mathbf{\Sigma }}_{\theta }(x_t,t)$는 일반적으로 $x_t$와 $t$를 입력으로 출력을 생성하는 인공신경망으로 정의된다.

 

4. 목적 함수 및 학습 알고리즘

DDPM의 목적은 reverse process를 통해 새로운 데이터를 생성하는 것이기 때문에 DDPM은 아래와 같이 확률분포 $p_{\theta }(x)$의 log-lilkelihood를 최대화하도록 학습이 이루어진다.

$$\begin{array}{}\text{(6)}& {\theta }^{\ast }=\underset{\theta }{\text{argmax}}\mathbb{E}[\log p_{\theta }(x)].\end{array}$$

대부분의 문제에서 DDPM의 목적 함수를 바로 계산하는 것은 불가능하기 때문에 아래의 과정을 통해 목적 함수의 하계 (lower bound)를 구하고, 하계를 최대화함으로써 DDPM의 학습을 진행한다.

$$\begin{array}{rl}\log p(x)& =\log \int p(x_{0:T})d{x}_{1:T}\\ & =\log \int \frac{p(x_{0:T})q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)}d{x}_{1:T}\\ \text{(7)}& & \ge {\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_{0:T})}{q(x_{1:T}|x_0)}]:=J.\end{array}$$

DDPM의 모델링에 해당하는 식 $\text{(1)}$과 $\text{(3)}$에 의해 목적 함수의 하계 $J$는 아래와 같이 계산 가능한 형태로 변형된다.

$$\begin{array}{rl}J& ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)\prod _{t=1}^T{p}_{\theta }(x_{t-1}|x_t)}{\prod _{t=1}^{T}q(x_t|x_{t-1})}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)p_{\theta }(x_0|x_1)\prod _{t=2}^T{p}_{\theta }(x_{t-1}|x_t)}{q(x_1|x_0)\prod _{t=2}^{T}q(x_t|x_{t-1})}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)p_{\theta }(x_0|x_1)\prod _{t=2}^T{p}_{\theta }(x_{t-1}|x_t)}{q(x_1|x_0)\prod _{t=2}^{T}q(x_t|x_{t-1},x_0)}]\\ & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)p_{\theta }(x_0|x_1)}{q(x_1|x_0)}+\log \prod _{t=2}^T\frac{p_{\theta }(x_{t-1}|x_t)}{\frac{q(x_t,x_{t-1},x_0)q(x_t,x_0)q(x_0)}{q(x_{t-1},x_0)q(x_t,x_0)q(x_0)}}]\\ \text{(8)}& & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)p_{\theta }(x_0|x_1)}{q(x_1|x_0)}+\log \prod _{t=2}^T\frac{p_{\theta }(x_{t-1}|x_t)q(x_{t-1}|x_0)}{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}].\end{array}$$

식 $\text{(8)}$의 두 번째 항을 전개하면, $\text{(8)}$은 아래와 같이 정리된다.

$$\begin{array}{rl}J& ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)p_{\theta }(x_0|x_1)}{q(x_T|x_0)}+\sum _{t=2}^T\log \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}]\\ \text{(9)}& & ={\mathbb{E}}_{q(x_{1:T}|x_0)}[\log p_{\theta }(x_0|x_1)]+{\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p(x_T)}{q(x_T|x_0)}]+\sum _{t=2}^T{\mathbb{E}}_{q(x_{1:T}|x_0)}[\log \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}].\end{array}$$

기댓값의 정의와 DDPM의 Markov 속성을 이용하면 $q(x_{1:T}|x_0)$에 대한 기댓값을 아래와 같이 정리할 수 있으며, 이를 통해 실제 목적 함수를 계산하기 위해 어떠한 샘플을 추출해야하는지를 명확히 할 수 있다.

$$\begin{array}{}\text{(10)}& J={\mathbb{E}}_{q(x_1|x_0)}[\log p_{\theta }(x_0|x_1)]+{\mathbb{E}}_{q(x_T|x_0)}[\log \frac{p(x_T)}{q(x_T|x_0)}]+\sum _{t=2}^T{\mathbb{E}}_{q(x_t,x_{t-1}|x_0)}[\log \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}].\end{array}$$

Kullback–Leibler divergence $D_{KL}$의 정의에 의해 최종 목적 함수는 아래와 같이 정의된다.

$$\begin{array}{}\text{(11)}& J=\underset{\text{reconstruction term}}{\underbrace{{\mathbb{E}}_{q(x_1|x_0)}[\log p_{\theta }(x_0|x_1)]}}-\underset{\text{prior matching term}}{\underbrace{D_{KL}(q(x_T|x_0)||p(x_T))}}-\sum _{t=2}^T\underset{\text{denoising matching term}}{\underbrace{{\mathbb{E}}_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))]}}.\end{array}$$

따라서, DDPM의 매개변수 $\theta$는 식 $\text{(11)}$을 최대화함으로써 학습된다.

 

5. 목적 함수의 의미

DDPM 학습의 목적 함수인 식 $\text{(11)}$의 각 항은 아래와 같이 해석될 수 있다.

• Reconstruction term: 주어진 데이터 $x_0$에 대해 $x_1$를 생성하고, 다시 $x_1$을 이용하여 $x_0$를 생성함으로써 계산할 수 있다. 이는 variational autoencoder (VAE)의 동작과 유사하며, 이러한 해석을 바탕으로 첫 번째 항을 reconstruction term으로 간주할 수 있다.
• Prior matching term: forward process의 최종 출력에 대한 분포 $x_T$와 식 $\text{(4)}$에서 가정한 $x_T$의 사전 분포의 차이를 의미한다. 그러나 두 번째 항에는 학습 가능한 매개변수가 없기 때문에 DDPM의 학습 과정에서는 상수로 취급된다.
• Denoising matching term: 노이즈를 제거해나가는 과정 $p_{\theta }(x_{t-1}|x_t)$를 학습한다. $q(x_{t-1}|x_t,x_0)$는 최종적으로 노이즈가 제거된 데이터 $x_0$가 주어졌을 때의 노이즈 제거 과정을 의미하기 때문에 $q(x_{t-1}|x_t,x_0)$는 $p_{\theta }(x_{t-1}|x_t)$를 학습시키기 위한 ground truth 정보로 볼 수 있다.

 

6. 정규분포 가정 기반의 목적 함수 변형

복잡한 과정을 거쳐 DDPM의 목적 함수인 식 $\text{(11)}$을 유도했지만, 현재 상태로 목적 함수를 계산하는 것은 매우 어렵다. DDPM에서는 식 $\text{(2)}$과 $\text{(5)}$의 정규분포 가정을 바탕으로 식 $\text{(11)}$을 계산 가능한 형태로 변형한다.

먼저 Markov 가정에 의해 $q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})$로 생각할 수 있다. 그 다음 ${\alpha }_t=1-{\beta }_t$로 정의하면, 식 $\text{(???)}$의 정규분포 가정과 reparameterization trick에 의해 $x_t$를 아래와 같이 계산할 수 있다.

$$\begin{array}{}\text{(12)}& x_t=\sqrt{(}{\alpha }_t)x_{t-1}+\sqrt{(1-{\alpha }_t)}ϵ,\end{array}$$

위의 식에서 $ϵ\sim \mathcal{N}(ϵ;\mathbf{\text{0}},\mathbf{\text{I}})$인 랜덤값이다.

 

 

 

[1] Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. (2015, June). Deep unsupervised learning using nonequilibrium thermodynamics. In International conference on machine learning (pp. 2256-2265). pmlr.