B+ 트리의 개념은 B 트리와 같다. 그러나 B 트리는 entry sequenced file을 이용하여 데이터 파일을 표현하지만, B+ 트리는 indexed sequential file을 이용한다. Indexed sequential file의 장점과 구현 방법은 이전의 글에서 설명하였다.
B+ 트리는 인덱스로 indexed sequential file의 separator를 이용한다. Indexed sequential file의 separator는 유일하게 결정되는 것이 아니라, 같은 파일이더라도 다양한 separator가 정의될 수 있으므로, B+ 트리의 개념을 설명하기 위해 실제 key 값의 가장 짧은 prefix를 separator로 이용하는 simple prefix B+ 트리를 예로 들어 설명한다. 아래와 같은 indexed sequential file이 있을 때,
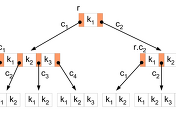
simple prefix B+ 트리는 아래와 같이 생성된다.
위와 같은 indexed sequential file을 갖는 B+ 트리에서 첫 번째 block과 두 번째 block을 구분하는 separator는 Bol, Boli, ..., Bolivia 등이 이용될 수 있지만, 위의 그림에 표현된 구조는 simple prefix B+ 트리이기 때문에 Bo를 separator로 이용한다.
위의 개요에 표현된 B+ 트리에서 6번째 block에 위치한 Poland를 제거하면, B+ 트리는 아래와 같이 변경된다.
B+ 트리에서 remove 연산은 해당하는 block에서만 변화를 야기한다. 즉, Poland 다음에 저장되어 있었던 Swiss가 block의 첫 번째 데이터로 변경되는 것을 제외하면, B+ 트리 전체에는 어떠한 변화도 발생하지 않는다. B+ 트리의 remove 연산이 갖는 이러한 단순함은 merge, redistribution 등과 같은 복잡한 연산을 빈번하게 수행해야 했었던 B 트리의 remove 연산에 비해 매우 효율적이다. 그러나 특정한 경우에는 B+ 트리의 remove 연산에서도 underflow가 발생한다. 이러한 경우에는 B 트리와 같이 merge, redistribution 연산을 이용하여 트리를 재구성하면 된다.
B+ 트리의 insert 연산은 B 트리의 insert 연산과 매우 유사하다. 아래의 그림은 B+ 트리의 insert 연산의 수행 과정을 나타낸다.
B+ 트리의 insert 연산은 B 트리와 마찬가지로 B 트리의 leaf node에 해당하는 block에 데이터가 추가된다. 그 다음, overflow의 발생 여부를 확인하여 overflow가 발생하였다면, parent node로 이동하여 overflow에 대한 처리를 수행한다.
B+ 트리에서 index set이라는 것은 각 block을 찾아가기 위한 separator들의 집합이다. 아래의 그림에서 푸른색으로 표시된 부분이 B+ 트리의 index set이다. 그림에서는 모든 separator가 하나의 index set에 포함되어 있지만, separator의 수가 많아지면 여러 index set block으로 분리하여 separator를 저장해야 한다.
B 트리에서 인덱스를 저장하는 각 노드는 고정된 수의 고정 길이 인덱스를 저장하기 때문에 고정 길이 데이터로 표현할 수 있었다. 그러나 B+ 트리의 index set은 가변 길이로 표현되는 separator를 저장해야 하며, 저장되는 separator의 수도 가변적이다. B+ 트리의 index set의 가장 큰 문제는 separator의 크기가 가변적이기 때문에 이진 탐색(binary search)를 이용할 수 없다는 것이다.
Index set의 이러한 문제를 해결하기 위한 방법으로는 separator의 리스트, 인덱스의 리스트, RBN의 리스트 등을 이용하는 방법 등이 있다. 아래의 그림은 인덱스의 리스트를 이용하여 index set에 이진 탐색을 적용할 수 있도록 index set를 구현한 것이다.
위와 같은 구조의 index set에서는 Separator는 가변 길이로 표현되어도 separator에 대한 인덱스는 고정 길이로 표현되기 때문에 인덱스에 이진 탐색을 적용하여 탐색을 수행하면 된다.
'객체지향설계' 카테고리의 다른 글
| [파일구조] - Indexed Sequential File (1) | 2016.06.12 |
|---|---|
| [파일구조] - Virtual B 트리 (0) | 2016.06.12 |
| [파일구조] - B 트리의 연산 (0) | 2016.06.12 |
| [파일구조] - B 트리 (0) | 2016.06.11 |
| [파일구조] - 트리 구조를 이용한 인덱스 관리 (0) | 2016.06.11 |